距离和相似度度量

6 条回复

　　在数据分析和数据挖掘的过程中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，如K最近邻（KNN）和K均值（K-Means）。当然衡量个体差异的方法有很多，最近查阅了相关的资料，这里整理罗列下。

　　为了方便下面的解释和举例，先设定我们要比较X个体和Y个体间的差异，它们都包含了N个维的特征，即X=（x₁, x₂, x₃, … x_n），Y=（y₁, y₂, y₃, … y_n）。下面来看看主要可以用哪些方法来衡量两者的差异，主要分为距离度量和相似度度量。

距离度量

　　距离度量（Distance）用于衡量个体在空间上存在的距离，距离越远说明个体间的差异越大。

欧几里得距离(Euclidean Distance)

　　欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

Euclidean Distance

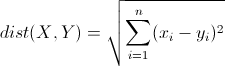
　　因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。

明可夫斯基距离(Minkowski Distance)

　　明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性的表述。公式如下：

Minkowski Distance

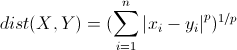
　　这里的p值是一个变量，当p=2的时候就得到了上面的欧氏距离。

曼哈顿距离(Manhattan Distance)

　　曼哈顿距离来源于城市区块距离，是将多个维度上的距离进行求和后的结果，即当上面的明氏距离中p=1时得到的距离度量公式，如下：

Manhattan Distance

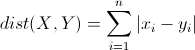
切比雪夫距离(Chebyshev Distance)

　　切比雪夫距离起源于国际象棋中国王的走法，我们知道国际象棋国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x₁, y₁)走到B格(x₂, y₂)最少需要走几步？扩展到多维空间，其实切比雪夫距离就是当p趋向于无穷大时的明氏距离：

Chebyshev Distance

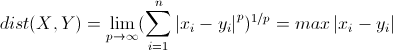
　　其实上面的曼哈顿距离、欧氏距离和切比雪夫距离都是明可夫斯基距离在特殊条件下的应用。

马哈拉诺比斯距离(Mahalanobis Distance)

　　既然欧几里得距离无法忽略指标度量的差异，所以在使用欧氏距离之前需要对底层指标进行数据的标准化，而基于各指标维度进行标准化后再使用欧氏距离就衍生出来另外一个距离度量——马哈拉诺比斯距离（Mahalanobis Distance），简称马氏距离。

相似度度量

　　相似度度量（Similarity），即计算个体间的相似程度，与距离度量相反，相似度度量的值越小，说明个体间相似度越小，差异越大。

向量空间余弦相似度(Cosine Similarity)

　　余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。公式如下：

皮尔森相关系数(Pearson Correlation Coefficient)

　　即相关分析中的相关系数r，分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角。公式如下：

Pearson Correlation Coefficient

Jaccard相似系数(Jaccard Coefficient)

　　Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度，因为个体的特征属性都是由符号度量或者布尔值标识，因此无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。如果比较X与Y的Jaccard相似系数，只比较x_n和y_n中相同的个数，公式如下：

调整余弦相似度(Adjusted Cosine Similarity)

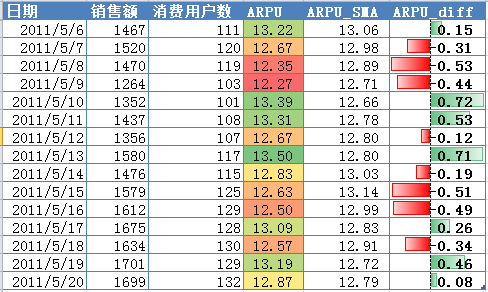
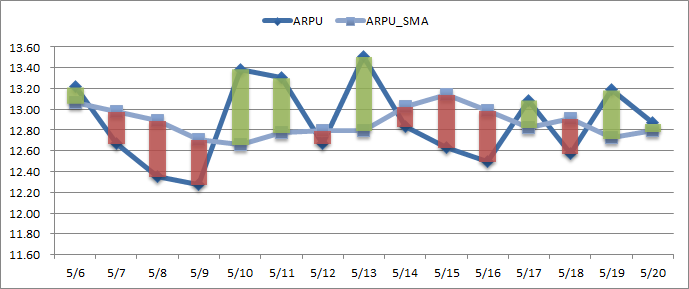
　　虽然余弦相似度对个体间存在的偏见可以进行一定的修正，但是因为只能分辨个体在维之间的差异，没法衡量每个维数值的差异，会导致这样一个情况：比如用户对内容评分，5分制，X和Y两个用户对两个内容的评分分别为(1,2)和(4,5)，使用余弦相似度得出的结果是0.98，两者极为相似，但从评分上看X似乎不喜欢这2个内容，而Y比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性，就出现了调整余弦相似度，即所有维度上的数值都减去一个均值，比如X和Y的评分均值都是3，那么调整后为(-2,-1)和(1,2)，再用余弦相似度计算，得到-0.8，相似度为负值并且差异不小，但显然更加符合现实。

欧氏距离与余弦相似度

　　欧氏距离是最常见的距离度量，而余弦相似度则是最常见的相似度度量，很多的距离度量和相似度度量都是基于这两者的变形和衍生，所以下面重点比较下两者在衡量个体差异时实现方式和应用环境上的区别。

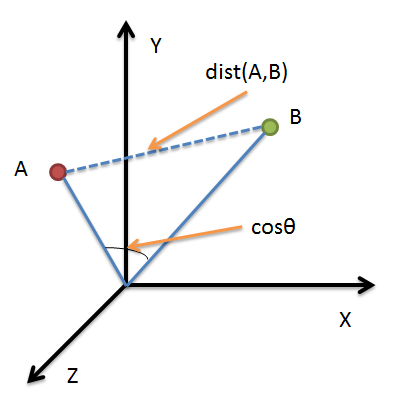
　　借助三维坐标系来看下欧氏距离和余弦相似度的区别：

　　从图上可以看出距离度量衡量的是空间各点间的绝对距离，跟各个点所在的位置坐标（即个体特征维度的数值）直接相关；而余弦相似度衡量的是空间向量的夹角，更加的是体现在方向上的差异，而不是位置。如果保持A点的位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦相似度cosθ是保持不变的，因为夹角不变，而A、B两点的距离显然在发生改变，这就是欧氏距离和余弦相似度的不同之处。

　　根据欧氏距离和余弦相似度各自的计算方式和衡量特征，分别适用于不同的数据分析模型：欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异；而余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦相似度对绝对数值不敏感）。

　　上面都是对距离度量和相似度度量的一些整理和汇总，在现实的使用中选择合适的距离度量或相似度度量可以完成很多的数据分析和数据挖掘的建模，后续会有相关的介绍。

比较测试的设定和分析

24 条回复

——数据的上下文5

　　基于前一篇文章——T检验和卡方检验中提出的数据比较方法，其实我们在生物或者化学的实验中经常也会涉及比较，这篇文章就来具体介绍如何在现实的网站分析环境中使用这些方法，使用的前提和环境是怎样的。

　　其实我们在做数据分析的时候经常进行比较分析，但往往以观察分析法为主，“T检验和卡方检验”为我们的比较分析提供了很好的科学的定量分析方法，让比较的结果更有置信度和说服力。但在使用定量分析的比较方法前，还有很多因素需要考虑，当我们需要精确地分析比较的效果，我们一般都会做比较测试，而其中涉及测试环境的设定，数据的选择和获取等，以排除一些非相关因素的干扰，让比较的结果更加真实可信，所以下面就介绍下如何合理地进行比较测试。

比较测试的类型

　　比较测试或实验的类型有很多，但都跳不出抽样、重复、分组、比较这几个流程，所以从实验设计的角度，我们可以简单地把比较测试分为两类：基于时间序列的组内比较和基于对照实验的组间比较。

时间序列的组内比较

　　基于时间序列的组内比较一般在时间序列上的某个时间点引入实验变量或者施加实验刺激，并在实验刺激的前后进行重复测试，分别叫做“前测”和“后测”，对前测和后测分别进行抽样比较，从比较的结果反映实验刺激是否对结果有显著的影响。详细的流程见下图：

　　举个有趣的例子，如果公司的员工前4个月在正常的薪资待遇的水平上工作，体现出正常的工作效益和工作满意度；然后从第5月开始给员工进行加薪（施加实验刺激），再观察之后4个月员工的工作效益和工作满意度，将之前4个月的结果（前测）与后4个月的结果（后测）进行比较，分析员工的工作效益和工作满意度是否存在显著性差异，进而证明加薪这个实验刺激是否对提升员工的工作效益和满意度有显著性影响。这就是简单的时间序列比较测试的基本流程。

　　但基于时间序列的比较测试会受很多因素的干扰，比如上面的例子在实验过程中CPI的增长、公司业绩的下滑或者运营环境的恶化都可能导致实验结果的失效，或者验证的结果不可信，所以下面会具体说明需要排除的干扰因素。

对照实验的组间比较

　　基于时间序列的组内比较只是基于一组样本，只是样本在时间序列的某个点上受到了实验变量的刺激；而对照实验需要设定两组样本，也就是“实验组”和“控制组”，并对实验组施加实验刺激，控制组维持原状态不变，从而比较实验组和控制组是否存在显著差异来反映实验的刺激是否影响了结果。因为对照实验涉及两组样本，所以这里需要额外注意抽样的规范性，我们需要保证两组样本的特征具有相似性，可以进行比较。具体的实验设计见下图：

　　还是使用上面的例子，但在对照实验中设置对照组和实验组是必需的，比较不再是基于前测和后测。比如我们让部分员工维持当前的薪资待遇继续工作，而另外一部分的员工提升他们的薪资待遇，从而比较为提升待遇的员工和提升待遇的员工的工作效益和工作满意度的差异，如果差异显著就可以证明提升薪资待遇这个实验刺激对结果是有显著影响的。

　　对照实验因为参与比较的两组样本都是基于相同的时间序列轴，所以随着时间变化的影响因素对实验的比较结果的影响不再重要，因为两组样本同时受到了同样的影响，但因为是组间比较，所以两组样本如果存在差异性，那么对结果就会造成较大影响，比如上例中A组选择的是基层员工，B组选择中高层员工的话，比较的结果显然是缺乏科学性的。下面就具体介绍下比较测试中可能存在的影响因素有哪些？

前提与影响因素

　　首先看一下从用户体验的角度，如果我们进行可用性实验，需要考虑的影响因素有哪些：

外部噪声和干扰：外部干扰信息、临时的电话和呼唤等；
经验和熟练：因为可用性实验一般需要重复过程，所以随着实验的进程，用户渐渐熟悉对网站和工具的使用；
消耗：随着实验进程，用户可能失去耐心，或者精力无法集中；
主观预测：当进行重复实验时，用户容易用先前的测试结果来推测之后的测试，同样会影响实验结果的可信度。

　　以上是可用性实验中需要考虑的影响因素，有些只存在于实验环境中，如果衍生到WEB分析中，同样需要注意一些影响因素，而对于上面介绍的时间序列组内比较和对照实验组间比较，各自的影响因素又各不相同：

时间序列的组内比较

　　基于时间序列的组内比较可能存在的干扰因素相对较多，因为外部环境和内部环境都会随着时间发生变化，所以为了让基于时间序列的前测和后测两组数据具有可比性，我们必须规避以下几类因素的影响：

数据本身存在的自然增长或下降趋势；
规避节假日或者外部事件的影响；
规避特殊的营销推广其带来的影响；
规避内部其他可能影响测试结果的因素（实验刺激必须唯一）。

对照实验的组间比较

　　对照实验因为两组样本处在相同的环境和时间序列上，所以需要规避的影响因素比上面要少很多，但相较组内比较，组间比较需要额外考虑两组样本是否具有可比性：

两组样本特征相似，可比较（抽样规范性）；
实验组跟对照组之间只存在唯一的实验刺激导致的差异。

　　无论是基于时间序列的组内比较还是基于对照实验的组间比较，都要规避外部环境的重大变动，或者特殊的外部事件对网站造成的重大影响，或者服务器故障或数据统计异常造成的数据不完整或不准确，因为这些因素造成的影响已经可能导致用于比较的数据本身就存在巨大误差，或者不可信，都是无法规避和弥补的。

网站应用实例

　　网站环境下最常见的比较测试显然就是A/B Testing，AB测试为网站的改版和优化提供了对照实验的比较测试环境，具体的流程如下：

　　访问网站的用户被AB测试的系统自动分成了两组，一般情况下是按比例对半划分，当然很多情况下也会根据需要按其他合适的比例，如1:3，1:5等。这里的A方案和B方案一个是未做改动的原方案，另一个是改版后的新方案，如果一次需要测试多个改进方案的效果，那么就需要设定多个实验组，而控制组只要一个就行。

　　A/B Testing属于对照实验的组间比较的测试方法，所以同样需要符合对照实验的前提，规避对照实验可能存在的其他影响因素。因为A/B Testing遵循了简单随机抽样的方法，所以我们可以认为实验组和对照组之间的样本无明显的差异，具有可比性。同时，对照实验基于相同的内外部环境和相同的时间序列，所以诸如节假日、数据自然增长或下降、特殊推广期等的影响可以不用考虑，但某些特别重大的外部事件或者网站服务器故障导致的数据问题还是需要在比较测试之前进行排除。另外对照实验中必须控制每个实验组的实验刺激只能是1个，不然无法区分到底是哪个实验刺激对实验结果造成的影响。

　　在规避上述影响因素后，基于A/B Testing的数据比较可以使用我在上篇文章中介绍的“T检验和卡方检验”的方法直接进行显著性的检验，进而验证实验刺激对结果是否存在显著性影响，这里不再重复举例了。

　　A/B Testing有自己的优势，它比基于时间序列的比较的限制因素要少很多，但A/B Testing毕竟需要预先构建相应的自动分流系统，可能在某些特定的环境下或者对某些特殊的网站而言没有相应的环境可以进行AB测试，这个时候我们就不得不选择时间序列的比较测试。

　　基于时间序列的组内比较需要规避推广、节假日和外部营销事件的影响，这个可以通过选择合理的测试起止时间，选择合适的前测和后测样本进行规避，但如果网站本身数据存在明显的上涨或下降趋势，那么我们必须对数据进行必要的处理：

改版前		改版后
用户数	订单数	用户数	订单数
12395	576	13920	704
13237	641	14391	715
13450	732	15692	781
13872	693	16533	839
14673	770	15916	813

　　上表是某电子商务网站基于时间序列改版前后的比较测试，前测和后测各选取5天的数据进行比较，以“订单数”作为比较指标，为了说明改版能不能显著地提升每天订单的数据。如果我们不考虑数据本身的自然增长，直接比较改版前后日均订单数的差异：

　　改版前日均订单数682.4 < 改版后日均订单数770.4

　　显然改版后日均订单有显著提升，说明改版有效？那么我们将数据的自然增长考虑进去，我们可以将日均用户数的增长率作为整个网站数据的自然增长率：

　　(改版后日均用户数 – 改版前日均用户数) / 改版前日均用户数 = 13.05%

　　改版前日均订单数682.4 * 1.13 = 771.1 > 改版后日均订单数770.4

　　比较的结果发生了改变，改版前的日均订单数在乘上自然增长率后要比改版后的日均订单数高，但相差不多，从结果看应该是改版对订单数的提升无显著影响。显然后面考虑网站自然增长率后的比较结果更加科学，更加可信和具有说服力。这就是我们在基于时间序列的比较测试中需要考虑的一些问题。当然上面是基于简单的观察分析比较，如果需要更具统计学意义的定量比较，同样可以对数据进行自然增长处理后使用T检验或者卡方检验。

　　这篇文章可能写得有点长，本来想分两篇发布，但因为内容不太好分段，也怕影响内容的连贯性，所以最终都整合到了一篇，希望大家有耐心能够看完。当然期间的一些看法如果有问题，或者大家有自己的其他见解，都可以在下面评论留言，非常欢迎大家提出其他的看法。一边在看羽毛球世锦赛男单决赛一边更新了这篇博客，希望文中不要存在过多地错误或者错别字

T检验和卡方检验

32 条回复

　　好久没有更新博客了，今天更新一篇关于数据分析方法的文章，主要是基于统计学的假设检验的原理，无论是T检验还是卡方检验在现实的工作中都可以被用到，而且结合Excel非常容易上手，基于这类统计学上的显著性检验能够让数据更有说服力。还是保持一贯的原则，先上方法论再上应用实例，这篇文章主要介绍方法，之后会有另外一篇文章来专门介绍实际的应用案例。

关于假设检验

　　假设检验（Hypothesis Testing），或者叫做显著性检验（Significance Testing）是数理统计学中根据一定假设条件由样本推断总体的一种方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。既然以假设为前提，那么在进行检验前需要提出相应的假设：

　　H0：原假设或零假设（null hypothesis），即需要去验证的假设；一般首先认定原假设是正确的，然后根据显著性水平选择是接受还是拒绝原假设。

　　H1：备择假设（alternative hypothesis），一般是原假设的否命题；当原假设被拒绝时，默认接受备择假设。

　　如原假设是假设总体均值μ＝μ₀，则备择假设为总体均值μ≠μ₀，检验的过程就是计算相应的统计量和显著性概率，来验证原假设应该被接受还是拒绝。

T检验

　　T检验（T Test）是最常见的一种假设检验类型，主要验证总体均值间是否存在显著性差异。T检验属于参数假设检验，所以它适用的范围是数值型的数据，在网站分析中可以是访问数、独立访客数、停留时间等，电子商务的订单数、销售额等。T检验还需要符合一个条件——总体符合正态分布。

　　这里不介绍t统计量是怎么计算的，基于t统计量的显著性概率是怎么查询的，其实这些计算工具都可以帮我们完成，如果有兴趣可以查阅统计类书籍，里面都会有相应的介绍。这里介绍的是用Excel的数据分析工具来实现T检验：

　　Excel默认并没有加载“数据分析”工具，所以需要我们自己添加加载项，通过文件—选项—加载项—勾选“分析工具库”来完成添加，之后就可以在“数据”标签的最右方找到数据分析这个按钮了，然后就可以开始做T检验了，这里以最常见的配对样本t检验为例，比较某个电子商务网站在改版前后订单数是否产生了显著性差异，以天为单位，抽样改版前后各10天的数据进行比较：

	改版前订单数	改版后订单数
1	1032	1187
2	1178	1245
3	1098	1379
4	1045	1094
5	976	1173
6	1101	1364
7	1276	1119
8	1215	1268
9	987	1303
10	1065	1274

　　首先建立假设：

H0：μ₁＝μ₂，改版前后每天订单数均值相等；
H1：μ₁≠μ₂，改版前后每天订单数均值不相等。

　　将数据输入Excel，使用Excel的数据分析工具，选择“t检验：平均值的成对二样本分析”，输出检验结果：

　　看到右侧显示的结果是不是有点晕了，看上去有点专业，其实也并不难，只要关注一个数值的大小——单尾的P值，这里是0.00565，如果需要验证在95%的置信水平下的显著性，那么0.00565显然小于0.05(1-95%)，拒绝零假设，认为改版前后的订单数存在显著性差异。简单说下为什么选择单尾显著性概率P，而不是双尾，对于大部分网站分析的应用环境，我们一般需要验证改动前后数值是否存在明显提升或下降，所以一般而言只会存在一类可能——或者提升或者下降，所以只要检验单侧的概率即可，就像上面例子中改版后的订单数均值1240.6大于改版前的1097.3，我们需要验证的就是这种“大于”是否是显著的，也就是做的是左侧单边检验，这种情况下只要关注单尾的显著性概率P即可。

卡方检验

　　卡方检验（chi-square test），也就是χ²检验，用来验证两个总体间某个比率之间是否存在显著性差异。卡方检验属于非参数假设检验，适用于布尔型或二项分布数据，基于两个概率间的比较，早期用于生产企业的产品合格率等，在网站分析中可以用于转化率、Bounce Rate等所有比率度量的比较分析，其实在之前的文章——Abandonment Rate的影响因素进行过相关的应用。这里同样不去介绍χ²是如何计算得到的，以及基于χ²统计量的显著性概率的查询等，这里直接以转化率为例来比较网站改版前后转化率是否发生了显著性差异，抽样改版前后各3天的网站分析数据——总访问数和转化的访问数，用“转化访问数/总访问数”计算得到转化率：

	改版前	改版后
总访问数	30567	33651
转化访问数	2976	3698
转化率	9.74%	10.99%

　　首先建立假设：

H0：r₁＝r₂，改版前后转化率相等；
H1：r₁≠r₂，改版前后转化率不相等。

　　其实这是一个最简单的四格卡方检验的例子，也无需使用SPSS（当然你足够熟悉SPSS也可以使用类似的统计分析工具），为了简化中间的计算步骤，我这里用Excel直接制作了一个简单的卡方检验的模板，只要在相应的单元格输入统计数据就能自动显示检验的结果：

点击下载：卡方检验示例

　　Excel中浅蓝色的单元格都支持输入，包括原用方案和测试方案的总访问数和转化访问数，另外置信度95%也是支持修改了，如果你需要99%的置信水平，只要修改这个单元格即可。

　　怎么看检验结果？其实非常简单，只要看那个红色的“存在”单元格的显示结果即可，上面的案例中两者的转化率“存在”显著性差异，如果不存在，则该单元格相应的就会显示“不存在”，有了这个模板对于A/B Testing等类似的数据比较也显得非常简单容易，或者说其实这个Excel模板就是为了A/B Testing而量身定制的。

　　好了，就到这里吧，其实这篇文章并不是想从专业的统计学的角度来介绍T检验和卡方检验，只是想让大家了解这两个方法的原理和适用条件，能够用最简单的方式去使用诸如此类的方法让数据更具说服力，请继续关注之后奉上的应用实例。

合并和比较度量

8 条回复

——数据的上下文4

　　往往我们在做分析的时候需要结合各类基本的指标进行二次计算合并得到一个可以用于进行综合评价或比较的度量，这个过程中就需要涉及到一些指标的合并技巧，和比较基准的设定。其实之前“数据上下文”的系列文章中也一再强调了我们需要为指标设定合理的参考系来评价指标的趋势或表现的好坏，之前提供了一系列的方法，但这篇文章里面要介绍的方法应该是最简单方便的，同时不失实用性，得益于《用户体验度量》这本书中的介绍，所以这篇文章更像是一篇读书笔记，内容基本整理总结自《用户体验度量》第8章——合并和比较度量，当然不再局限于用户体验层面，结合了网站分析层面的思考。

　　这里我根据合并和比较类型的不同将内容分成：简单合并度量目标比较、百分比评分度量均值比较、标准化度量组间比较和与专家绩效的比较。

简单合并度量目标比较

　　这是一个最简洁有效的KPI评价模式。首先说下简单合并，举个例子，电子商务网站每天产生很多订单，这些订单由许许多多的网站访问带来，一旦某个访问产生了订单，我们就说这个访问产生了转化，所以最基础的统计指标没有转化率，只有网站的访问量和订单数，转化率是由“订单数/访问数”计算得到的。那么为什么要计算转化率，用订单量来评价网站绩效不是也可以吗？很简单，因为订单量会受到网站访问量的影响，而很多时候网站的访问量无法控制，所以我们不能说100次访问产生的10个订单一定比150次访问产生的15个订单要差，如果用着两个指标的合并度量——转化率来评价，显然更科学，因为都是10%，两者的绩效是相当的。

　　因为合并度量，如转化率、人均消费等指标一般较为稳定，波动幅度不会太大，我们一般会将这些指标作为网站的KPI，同时我们会为每个KPI设定一个预期的目标，比如我们设定网站的转化率目标是10%，那么我们来看看网站一个月内的目标达成比例有多高：

　　我们可以看到在5月份的31天时间里，有26天的转化率等于或者超过了目标值，从而目标的达成率就是83.87%（26/31），还算是一个不错的成绩。也许你的团队正在抱怨KPI太过苛刻，毕竟数据会受诸多因素的影响，要保证每天10%以上确实有难度，如果真能完全做到，那就是目标的设定过低，目标永远应该临界于可以达成和不能达成之间才是合理的，所以这里使用目标达成率来评估可能会更加合理。

百分比评分度量均值比较

　　但是有的时候我们没法为每个指标设定目标，毕竟目标更多的是为了控制网站的整体绩效或者KPI，对于一些基于细分的度量，我们需要使用另外的合并和比较方法，所以就有了基于百分比的评分。

　　同样很简单，百分比评分就是将指标的值都转化成百分比的形式，相当于该指标在100分制的条件下的得分有多少。如何将指标转化成为百分比的数值，一个很简单的方法就是所有的指标处于总体的最大值，这个方法对于所有大于0且分布不是特别离散的指标都是有效的。比如我们评价网站商品的质量，权衡商品的浏览量和转化率这2个指标，我们知道转化率本身就是一个百分比，但显然也是需要进行转化的，所以我们将每个商品的浏览量和转化率分别除以总体浏览量最大值和总体转化率最大值得到相应的百分比评分：

	浏览量	转化率	浏览量评分	转化率评分	评分均值
商品A	563	7%	100	78	88.9
商品B	121	9%	21	100	60.7
商品C	87	8%	15	89	52.2
商品D	367	5%	65	56	60.4

　　上面的均值基于简单平均的计算，同样我们可以对各指标引入权重进行加权平均，比如我们分别给浏览量评分和转化率评分分别赋予40%和60%的权重：

	浏览量	转化率	浏览量评分	转化率评分	加权评分均值
商品A	563	7%	100	78	86.7
商品B	121	9%	21	100	68.6
商品C	87	8%	15	89	59.5
商品D	367	5%	65	56	59.4

　　这样我们就可以根据最终的评分均值寻找那些高质量的商品进行推荐了。

标准化度量组间比较

　　又是标准化，是不是有点看腻了，但确实它在指标合并的领域扮演着极其重要的角色，同样推荐阅读——数据的标准化这篇文章。

　　方法这里不再详细介绍，还是举个例子，另外值得注意的一点就是对“逆指标”的处理，逆指标指的是那些表现的值刚好与绩效相反的指标，即值越大绩效越差，值越小绩效越好，网站分析中典型的逆指标就是Bounce Rate。因为标准化后的指标符合均值是0标准差是1的正态分布，所以对逆指标的处理只需要对标准化后的数据乘-1就可以了，也非常简单。这里以网站Landing Page优化为例，来看看如何有效地评价3个Landing Page的优化方案哪个才是最优的：

	Bounce Rate	转化率CR	BR标准化	CR标准化	标准化均值
方案A	45%	8%	-0.651	0.873	0.762
方案B	46%	5%	-0.501	-1.091	-0.295
方案C	57%	7%	1.151	0.218	-0.467

　　同样使用了求均值的方法，将各指标标准化后取均值进行比较（注意这里取均值时对BR标准化的结果乘了-1），我们就可以轻而易举的看出A方案的效果是最优的，这也是一种“目标决策”的最简单应用。这里需要注意的是指标标准化后的数值的分布是不定的，不像上面的百分比一定是在[0,100]之间，所以标准化后的数值本身不具有实际意义，只有将它放入比较环境中才有分析的价值，所以指标标准化的方法只适用于组间的比较。

与专家绩效的比较

　　如果你能够得到一个对该领域的专业知识和技能非常熟悉的专家团队的支持，那么对网站的评价会容易许多，因为专家对网站的使用和评分就可以作为网站的最优标准。

　　其实一般情况下我们认为专家的绩效是一个理想化的状态，比如专家能够在最短时间内通过最少的操作完成预期的任务，所以我们可以将专家组的数据作为网站可以达到的优化目标，而目前数据与专家数据的差异就是目前网站存在的优化空间，这样的分析让我们能足够明确自身在哪些模块距离最优的水平最远，同时优化的空间最大，我们完全可以从这些方面入手来实现最快最大的提升。

　　除了介绍以上的度量合并比较的方法外，书中还介绍了使用柱状折线组合图和雷达图来展现多指标的比较环境，因为这些在之前的文章中都有提及，这里不再介绍了。

　　其实上面介绍的都是最简单实用的指标比较处理的方法，这些方法无论在哪类公司或者哪些指标上都能够进行套用，甚至基于这些最基本的取百分比、取平均、目标比较等方法可以举一反三扩展出更加灵活有效的分析方法。这时候就需要动用你的智慧，为你的数据选择最合适的方法了。

指标的移动平均

6 条回复

——数据的上下文3

　　接着之前数据上下文（Context）的话题继续探讨网站分析中可以设立的数据意境。数据上下文2中的网站质量控制图为网站的KPI指标给出了有效的监控体系，但质量控制图毕竟比较严谨，其实对于大部分互联网环境的指标而言，可能并不符合这么苛刻的条件，于是我们需要寻找另外的方法来监控和观察这些指标的变化趋势。

　　同样是基于时间序列的分析，前面的文章——时间序列的趋势分析中主要介绍了“同比”和“环比”的概念，这里在介绍一种方法——移动平均法。其实移动平均线应用最多的是在股市，5日、10日、30日均线都是用移动平均法计算得到的；而移动平均线也是Excel中的趋势线的一种类型。所以移动平均法最常见的用法就是对于趋势变化的观察分析，但同时也具备了预测和比较监控的功能。下面介绍两个最简单常用的移动平均法：简单移动平均法（Simple Moving Average）和加权移动平均法（Weighted Moving Average）。

移动平均的适用条件

　　移动平均（Moving Average）是一种简单平滑预测技术，通过在时间序列上逐项推移取一定项数的均值的方法来表现指标的长期变化和发展趋势。因为取的是一定项数的均值，所以使用移动平均的指标需要满足以下几个条件：

指标没有明显的快速增长或下降的趋向
指标不具备周期性波动的特征

　　移动平均的最重要目的是消除指标的随机波动，如果指标不满足以上的两个条件，可能移动均值的平滑能力无法对指标做出准确的预测，那么移动平均也就失去了它的效用。移动均值主要基于对历史数据的平滑来预测实际数据，所以一方面对于历史数据过度依赖，另一方面对于现实的变动不够敏感，尤其是在使用多期均值时，这也是移动均值的两个缺点。

简单移动平均法

　　简单移动平均（Simple moving average, SMA），将时间序列上前n个数值做简单的算术平均。假设用X₁到X_n来表示指标在时间序列上前n期中每一期的实际值，那么第n+1期的预测值可以用以下公式来计算得到：

X_n+1 = ( X₁ + X₂ + …… + X_n ) / n

　　在Oracle数据库可以使用开窗函数直接计算得到简单移动平均值，比如要从每天的销售表（sales）计算近10天销售额（amount）的移动平均数与每天的销售额进行比较，可以用如下的PL/SQL实现：

SELECT date_id “日期”,SUM(amout) “每天销售额”,AVG(SUM(amount)) OVER(ORDER BY date_id ROWS BETWEEN 10 PROCEDING AND CURRENT ROW) “销售额移动均值” FROM sales GROUP BY date_id ORDER BY date_id;

　　Oracle内置了一堆的分析函数可以调用，直接用于各类的聚合和分析指标的计算，非常方便。

加权移动平均法

　　加权移动平均（Weighted moving average, WMA），在基于简单移动平均的基础上，对时间序列上前n期的每一期数值赋予相应的权重，即加权平均的结果。基本思想是：提升近期的数据、减弱远期数据对当前预测值的影响，使预测值更贴近最近的变化趋势。我们用W_n来表示每一期的权重，加权移动平均的计算公式如下：

X_n+1 = W₁×X₁ + W₂×X₂ + …… + W_n×X_n

　　这里需要满足W₁+W₂+……+W_n=1，对于各权重的确定，可以使用经验法根据需要进行赋权：如果希望预期值受前几期数据的影响逐步加深，则可以赋予递增的权重，如0.1,0.2,0.3……；如果希望加深最近期的几个数值的影响，以反映最近的变化，则可以适当加大近1-2期的权重，根据适应实际情况结合测试来完成赋权。我们来比较下简单移动平均（下图SMA线，取近5期均值）和加权移动平均（下图WMA线，取近5期加权均值，权重依次为0.1, 0.1, 0.2, 0.3, 0.3）：

　　可以看到无论是简单均值线还是加权均值线都要比实际值的波动小了很多，也就是平滑的效果，更多的是展现一个大体的趋势，而加权平均相较于简单平均的差异就在于加权平均更加注重近期的影响，所以这里的WMA绿线比SMA的红线更贴近前两期的数值趋势。

移动平均实例

　　还是结合实际的例子来做下说明。在电子商务数据分析里面，我们最关注的就是每天的销售额，我们用Excel里面的移动平均的趋势图可以反映出指标的变化趋势：

——3周期移动平均（虚拟数据）

　　上面展现的是移动平均法的用途之一——分析趋势，其实我们也可以用移动平均来进行数据监控和预警。

　　用移动平均法可以计算得到一个本期的预测值，我们可以将这个预测值作为本期预期可以实现的量，并用这个预期量与实际量进行比较，要分析实际量与预期量之间的差距。还是基于销售额，不过销售额可能存在明显的递增或递减趋势，于是我们除以消费用户数，于是就得到了所谓的ARPU值（Average Revenue Per User），这个是电子商务乃至任何消费型网站的关键指标之一，还是使用简单移动平均来比较实际值和预期值的差异：

——ARPU监控表格效果（虚拟数据）

　　表格的数据展现已经可以一目了然的看到实际ARPU值与预期的差异、差异的大小等，下面再结合图表来看一下：

——ARPU监控图表效果（虚拟数据）

　　两条比较的折线结合绿涨红跌的蜡烛图，能够对指标的变化情况了如指掌。结合上面的表和图的数据和效果，似乎对于数据的监控变得简单很多，即使是直接的观察也能快速地发现数据的异常，这些方法对于网站的一些关键指标，诸如转化率、人均消费、活跃度等指标的日常监控分析非常实用和有效。

　　如果你认为这些表和图对于指标监控还不够，那么就建一套自动的Alert系统吧，就像Google Analytics上面的Intelligence一样，如果指标的降幅或者涨幅超过正常范围（可以设定一个合理的阈值）就向你的邮箱发送报警邮件，这个对于敏感数据的监控异常有效。

　　我要介绍的就是这些了，切忌所有的方法和数据的处理都要根据实际的环境、具体的业务和运营状况来进行设定和分析，这里只是我的想法和对移动平均法的简单应用，在不同的环境下也许还可以扩展出许多不同的应用。你是不是也在用类似的方法？欢迎与我分享

网站的迷失度度量

16 条回复

　　在博客之前的文章——优化网站信息架构我曾经提到过关于迷失用户（Lost Visits）的定义，以及如何使用Google Analytics的高级群组（Advanced Segment）去区分出这批用户。最近在看《用户体验度量（Measuring the User Experience）》，发现自己实在太嫩了，人家Smith早在1996年就对迷失度（Lostness）有了定义，同时给出了迷失度L的计算公式，这里借花献佛，分享给大家。

即，L = sqrt[ (N/S-1)² + (R/N-1)² ]

L：迷失度

N：访问的不同页面数（Unique Pageviews）

S：访问的总页面数（Pageviews）

R：完成任务必需的最小页面数

　　Smith同时给出了迷失度的评定标准：最佳迷失度为0，迷失度小于0.4时，用户不会显示任何可观察到的迷失特征；迷失度大于0.5时，用户显现迷失特征。

　　结合公式，我们可以看到这里对迷失度的定义主要考虑到的是：1、重复访问相同的页面，2、没有能够用最简单的方式完成任务，过多地在网站中徘徊。其实第一眼看去这个公式有一定的道理，但细想一下其实也存在着不合理的地方。通常我们需要去获取知识，阅读和总结他人的经验，但如果只是一味地套用书本或者别人的东西，那么你就输了，尤其是在发展如此迅速的互联网领域。那么我们来看看这个公式有何不妥：

　　我们先思考这样一个问题：迷失的用户会表现怎样的特征？显然，当用户在网站中找不到自己需要的东西的时候会来回地点击各种页面，频繁地返回首页或者索引页面，那么从这个角度看，显然这个公式是成立的，迷失用户的表现特征就是频繁地重复浏览同一页面，并且浏览的页面数会比正常访问多得多。但再换一个角度思考，逆向思考下前面的问题：一个正常的用户会不会出现重复浏览同一页面或者浏览页面数较多的情况？显然也是可能的，简单的例子，如果你对我的博客非常感兴趣，看了一篇文章后还想看另外的文章……于是你来回于博客的文章页面和文章专题推荐或者网站地图页面之间，于是这些列出了文章索引的页面被一次又一次地重复访问着；再如，如果一个用户上电子商务网站的目的不是购物，而是闲逛，看看有没有便宜货，或者只是针对某类商品比对下商品的好坏及价格的差异，以伺机下手，那么这个时候这些用户的访问页面数就会异常的多，但他们其实都没有迷失。所以，上面的公式无法为你从所有的用户中挑出那些迷失的用户，最多只能对已知的迷失用户计算他们的迷失度，哪些是低度迷失，哪些是高度迷失。

　　但其实Smith没有错，错的是这个高速发展的时代，这也是我为什么说尤其在互联网领域不要直接照搬一些东西来直接应用于自身的原因。1996年，很明显还处于WEB1.0时代，完全没有现在网站的那些复杂交互和多样的功能，当时的网站大部分做的只是信息的单向发布，而用户访问网站的任务也是单一的，可能就是查找到自己想要的那个信息页面。所以我反而觉得这个迷失度公式在当时绝对是适用的，而且Smith在当时就能总结得出这个的度量公式足见其对如今大热的“用户体验”的先知先觉以及对用户体验度量的智慧。同时这个公式对于当前网站的迷失度衡量也不是完全无效，如果是用户体验的小组在做可用性实验，为实验设定的情景是需要用户在网站中完成一个特定的任务，那么这个公式完全是有效的，所以总结起来就是这个公式对复杂的多任务的网站迷失度衡量无效，而对基于单任务的简单网站或者实验环境是有效的。

　　既然这个公式对于当前的网站大部分时间不适用，我们就需要对其进行改良，使其适用于普遍的网站。再观察下这个公式，我们会发现其实它跟数据挖掘里面的欧几里得距离度量的计算方式十分相似，可以理解为所有的比例为1时是最理想的状态，公式计算的结果就是每个样本点与这个1的理想点的距离，距离越近迷失度越低，距离越远迷失度越高。所以这个思路完全可以借鉴，但显然只考虑浏览页面的这些度量还不够，我们需要加入其他的网站分析度量。

　　对于现在的大部分网站而言，功能是多样化的，用户使用网站的任务不再是单一的，所以无法为不同任务的用户确定一个统一的完成任务的最小访问页面数，而公式的前半部分依然有效，我们尝试用其他度量来替换后半部分。于是自然而然的想到了停留时间，当用户没有迷失时他们会在自己感兴趣的页面停留一段时间，那么页面平均停留时长（Avg. Time on Page）不会很小，所以改进后的公式如下：

即，L = sqrt[ (N/S-1)² + (T/R-1)² ]

L：迷失度

N：访问的不同页面数（Unique Pageviews）

S：访问的总页面数（Pageviews）

T：访问页面的平均停留时间（Avg. Time on Page）

R：网站正常的页面平均停留时长（既定值）

　　这个公式同样有几点需要注意，首先N/S和T/R要保证小于等于1，这样迷失度L计算的结果才会落在[0,sqrt(2)]之间，才有评定是否迷失的可行性。N/S可以保证小于等于1，但T/R无法保证，所以再套用公式之前需要做一步数据筛选的工作，也就是过滤那些可以被简单认定不是迷失的访问（建议过滤访问页面数小于3或者页面平均停留时间大于R的所有访问），筛选后的所有访问即是需要去认定是否具有迷失倾向的访问，同时有保证了T/R小于等于1这个规则。至于R的值如何确定，可以先看一下你自己网站的几个数据：

　　从近一个月的数据观察，我的博客的页面平均停留时间（Avg. Time on Page）为2分钟半左右，所以我暂定公式中的R（网站正常的页面平均停留时长）为2分钟，用高级过滤器查看所有Time on Page小于2分钟的访问大概占到了网站所有访问的45%。同时，上图给出的3个指标恰恰就是公式中需要用到的上需要用到的3个指标，结合刚刚给定的R值，公式中所有需要的变量我们都已经可以拿到了，下面来看看几个示例：

序号	N	S	T	R	L
1	4	5	60	120	0.5385
2	5	8	25	120	0.8760
3	4	5	20	120	0.8570

　　上表中计算得到了3个访问样本的迷失度度量L的值，很显然我们当前没法判定到底哪个迷失了哪个没有，所以还缺少一个判定基准（Benchmark），正如上面Smith给出的0.4和0.5，因为公式的变更我们可能需要重新定义这个基准。当然，如果你要用非常严谨科学的态度去定义这个基准线的话，这个过程完全可以作为一个研究课题，进行可用性的实验，观察实验用户的迷失情况，结合每个实验用户的指标数据最终给出一个迷失度的判断基准。当然如果你有兴趣，这个完全可以作为你的毕业设计或者学校科研课题去展开研究，我这边没有时间和资源去完成这个庞大的项目，只能按照经验值进行预估，针对我的博客，我认为当用户的重复访问页面比例超过1/3，并且页面平均停留时间不到30秒时，用户可能已经表现出一定的迷失倾向，将这个数值代入公式得到的迷失度L的值约为0.82，那么这个就可以作为衡量用户迷失的一个基准线，当L大于0.82时用户表现迷失的倾向，小于0.82则为正常访问。

　　当然我这里提出的迷失度度量公式同样存在优化空间，如果你有更好的想法，可以一起交流，欢迎在评论里面提出你的想法。

　　可能这篇文章的中间写了一大堆“废话”，主要是自己当时看到这个公式时思考如何将它有效地应用到实际的一个过程，实在没有耐心的朋友可以直接跳过，不影响文章的整体实现思路，不要抱怨：“怎么不早说，现在才提，我看都已经看下来了”，如果你看完了，就证明你有一颗足够淡定的心。其实我自己觉得在获取信息的时候（无论是看书还是看网上的文章）思考过程才是最重要的，这是对信息的一个有效过滤的过程，只有思考之后你获取的信息才是优质的，才是被你真正吸收的。但也有一个弊端，就是发现自己看书实在太慢太拖沓，现在手上正在阅读的有4本书，都是现在进行时，每本书的进度在1/3到1/2不等，涉及数据分析、用户体验、数据挖掘和报表展现，精力不够集中，一段时间不能同时兼顾太多呀，反而拖慢进度。

网站内容评分模型

12 条回复

　　我们可以看到目前很多的网站都会有内容评分，无论是电子商务、信息分享还是内容下载。内容的评分主要分为两类，一类是用户对内容的评分，主要针对用户的使用感受，如电子商务网站的商品评分，内容分享网站的内容评分等，这个也是目前最普遍的评分模式，而内容的综合评分的计算也相对比较简单，大多是取所有用户评分的均值；另一种评分方式就是网站自身对内容的评分，主要针对用户的历史行为数据，如通过用户对内容的访问情况评价内容的热门程度等。

　　这里要介绍的网站内容评分模型主要针对第二类的评分方式，因为评分的分值是相对固定的，100分制、10分制还是5分制，而用户相对于每个内容所产生的行为数据的数值却千差万别，可能是千数量级，也可能是万数量级，甚至是百万数量级，如何将这些数据转化成标准的评分体制，并让最终的分值分布更加合理化、有效化，从而让真正优质的内容获得较高的评分，并推荐给用户，是这里重点要解决的问题。

内容评分实例

　　介绍应用的案例前，先要说明下应用的环境和具体的需求：假设有一个内容分享网站，需要将网站中的内容进行评分，以5分制的形式展现，即每个内容的评分只可能出现1-5这5个分值，目的是展现出网站中每个内容的热门程度，为用户的选择和阅读提供参考。

　　这是一个最简单的内容评分的应用，上面已经非常明确的说明了评分的目的——区分内容的热门度，以及最终的数据展现——以5分制的形式展现。对于这样一个明确了的数据需求，我们就可以选择指标、搭建模型、并最终输出结果。

1、选择指标

　　评价内容的热门度，貌似挺简单的，直接用内容浏览量（PV）作为评定指标不就行了？确实，PV是个不错的选择，也是最简单的一种选择，但其实还有更好的选择，访问数（Visits），访问用户数（UV），这两个指标能剔除同一个用户短时间内连续刷新同一内容的情况，所以我们不妨选择访问用户数UV来作为评价指标。

2、构建评分模型

　　现在开始才是文章的关键内容，显然，需要对内容的热门程度进行评价首先要消除指标的度量单位，并把分值的分布区间控制在要求的范围内——1-5分。

　　消除度量单位？也许你已经想到了，是的，还是数据的标准化，这篇文章中的方法已经在多处使用，可以说是很多数据分析和数据挖掘的基础步骤。

Min-Max归一化评分

　　Min-Max是最常用的数据归一化方法（详见数据标准化这篇文章的描述），处理后的数据分布在[0,1]的区间内，接下来只要把0-1的数值转化1-5这5个分值就行。很简单，先乘以4使数据落在[0,4]的分布区间，四舍五入，是不是只剩下0-4这5分分值了，再加1就可以得到我们想要的结果了。我们来看看处理后的各分值内容分布情况的示例：

　　根据上面各分值内容分布图可以看出Min-Max的评分结果的每个分值的内容数量分布是不可控的，一般会跟网站中热门内容和冷门内容的比例直接相关，所以当某些网站的热门内容只占网站所有内容的20%，并且这些内容的访问量异常高，占据了所有网站访问量的80%，也就是我们平常说的符合二八法则。那么可能出现的情况就是大部分的内容评分集中在1分，小部分集中在5分，而中间的2、3、4分的内容分布非常少，其实上图就有点偏向这个趋势，但其实很多时候我们期望的内容分布可以偏向正态，也就是大部分内容能分布在中间分值，两端分值的内容数据相对较少，于是就有了下面的另一种评分模型：

Z标准化评分

　　如果你的网站的内容数量很多，那么就可以使用Z标准化（详细描述还是参见数据标准化那篇文章，这里不重复了）。Z标准化的好处是可以让数据呈现正态分布的趋势（不是正是我们想要的吗），标准化后的数据趋于N(0,1)的正态分布，也就是整体的均值为0，标准差为1。再想想办法让他们变成只是1-5这5个分值，当标准化后的数值：

小于等于-1.5（即-1.5σ）时：1分

大于-1.5（即-1.5σ）小于等于-0.5（即-0.5σ）时：2分

大于-0.5（即-0.5σ）小于0.5（即0.5σ）时：3分

小于等于0.5（即0.5σ）小于1.5（即1.5σ）时：4分

大于等于1.5（即1.5σ）时：5分

　　如果数据符合标准正态分布，那每个分值的比例大概是，1分和5分的内容分别占7%，2分和4分的内容分别占23%，3分的内容占40%。我们再来看看用这个方法得到的评分结果的分布情况：

　　是不是看到你想要的结果了？

3、输出结果

　　当然内容评分的展现方式有很多，下面是几个网站的评分截图，其实都不错。

　　上面介绍的主要是针对单一指标的内容评分体系，其实在很多情况下内容的评分是诸多指标共同影响的结果，那么内容的评分应该考虑所有这些影响因子，应该构建相应的模型计算内容的综合评分，这里不展开，之后有机会再介绍。

值得关注的用户指标

24 条回复

　　最近最常被问到的就是一些用户的统计指标，无论是决策层还是产品部门，所以这篇文章重点说下用户指标的一些内容。

　　假设你想用尽量简洁有效的数据了解一个网站或产品的用户情况，你会问哪几个用户数据？其实一个聪明的提问者永远不会问网站的累计用户数有多少，甚至不会问网站的UV是多少，因为这些指标都不能从真正意义上去反映网站的价值和发展状况。

　　举个简单的例子——网秦，累计用户数应该不下千万，但这个数字真的能够体现网秦所具备的价值吗？按照网秦的这种运营推广模式，真正的活跃用户有多少，所占比例如何？3·15之后，流失用户又有多少，这个流失率是不是足以让网秦先前辛辛苦苦培养起来的用户基础毁于一旦？所以网秦的发展前景又如何？其实我们可以使用一些更有说服力的用户指标来反映这些情况。

用户的细分方式

　　我不建议把用户细分成许许多多的类型，目前为止见过的用户细分的类别也不在少数，罗列出来应该有一大串：当前用户、新老用户、活跃用户、流失用户、留存用户、回访用户、误闯用户、休眠用户、常驻用户、忠诚用户……其实很多的定义或含义是相近的，在分析层面也扮演着类似的指标角色。所以不建议将用户这样混乱无章地分成N个类别，用户的细分关键在于以合理的体系将用户细分成几个类别，并且每个类别都能发挥其在用户分析上的功效，不存在累赘和混淆。

　　所以这里想介绍下我认为比较合理的用户细分方式。我将用户分成以下几类：当前使用用户、新用户、活跃用户、流失用户、回访用户，下面来简单的解释下。

　　当前使用用户：即我们平常所说的UV，也就是网站的登录或者使用用户数。用于体现网站的当前运营状况。

　　新用户：首次访问或者刚刚注册的用户；那么那些不是首次来访的用户就是老用户，于是同时也获得了老用户的统计。用于分析网站的推广效果或者成长空间。

　　活跃用户数：活跃用户的定义千差万别，一般定义有关键动作或者行为达到某个要求时的用户为活跃用户；每个网站应该根据自身的产品特定定义活跃用户。活跃用户用于分析网站真正掌握了多少有价值用户。

　　流失用户：网站的活跃用户与流失用户中已经做了定义和介绍，用于分析网站保留用户的能力。我们将那些未流失的用户叫做留存用户，可以通过总使用用户数减去流失用户数计算得到。

　　回访用户：是指那些之前已经流失，但之后又重新访问你的网站的用户。用于分析网站对挽回流失用户的能力（常常会受到那些很久没有登录的网站给你发的邮件吧，让你回去看看，这些措施就是他们在挽留那些流失用户）。除非近期内执行了一些挽留流失用户的手段，正常情况下回访用户的比例应该是比较低的，否则就是你对流失用户的定义不够准确，应该适当延长定义流失的时间间隔。

　　所以其实在我们获得某些用户统计指标之后，通过计算同时也获得了诸如老用户、留存用户这些指标。

值得关注的用户指标

　　文章的开头已经提到过，如果你想了解一个网站或者一个产品的用户情况，请尽量抓住那些最为关键的用户指标。如果是我来问，我只会问3个指标：活跃用户数、新用户比例和用户流失率。

　　显而易见，活跃用户数直接反映了网站或者产品真正掌握着多少用户，这些用户并不是因为某些广告或者链接误点进来的，而是真正对这个网站或者产品感兴趣，有意向去使用或者持续关注的。活跃用户数越高，网站或者产品当前拥有的价值越高。但这里有一点需要格外注意，那就是活跃用户的定义，活跃用户跟新用户不一样，活跃用户可能催生各种形形色色的定义，之前的文章——用Engagement衡量用户活跃度对于如何定义用户活跃做过介绍，活跃用户的定义也类似，可以有各种方法。宽松的定义可以让活跃用户“变多”，比如只要访问页面数超过2页或者停留时间超过30秒；而严谨的定义可能会导致活跃用户“减少”，比如微博网站定义平均每天发送微博数量超过2条的才是活跃用户。所以，不同的定义影响着活跃用户的数量，当你问到活跃用户时，一定要了解对方是如何定义活跃用户的。我更偏向于严谨的定义，虽然这会让活跃用户“减少”，但严谨的定义让数据显得更加真实，可以说根据这个定义统计到的用户是那些真正在为网站创造价值的用户。

　　新用户比例反映着网站或产品的推广能力，渠道的铺设和带来的效果。新用户比例不仅是评估市场部门绩效的一个关键指标，同时也是反映网站和产品发展状况的重要指标。

　　但只看新用户比例是不够的，需要结合着用户流失率一起看。我见过流失率98%的网站，也见过流失率20%左右的产品，流失率会根据产品对用户黏性的不同而显得参差不齐。用户流失率反映了网站或者产品保留用户的能力，即新用户比例反映的是用户“进来”的情况，用户流失率反映的是用户“离开”的情况，结合这两个指标会有下面3类情况，代表了3种不同的产品发展阶段：

新用户比例大于用户流失率：产品处于发展成长阶段；

新用户比例与用户流失率持平：产品处于成熟稳定阶段；

新用户比例低于用户流失率：产品处于下滑衰退阶段。

　　下面附上一张反映活跃用户数、新用户比例和用户流失率的图表，你能从这张图中看出些什么，假如你是这个网站的CEO，你接下来需要从哪个角度重点着手来改善网站的运营状况？

　　这篇文章可能没有涉及任何的数据和分析，这里只想理清楚用户的细分和指标，当这套用户的细分和指标体系规范化了以后，能够让用户分析变得游刃有余。

排行榜与随机数

10 条回复

　　下面要介绍的内容也是前几天在工作中实际遇到并尝试去解决的一个问题。公司有一个优秀的团队，每个人都在思考如何解决目前存在的一些不合理的问题，无论是产品设计、内容运营还是后台架构。下面解决的问题就是源于一个数据的需求，根据需求进行设计和总结思考，同时也需要不断尝试着进行调整和优化。

　　其实无论是电子商务网站的商品交易量、内容网站的页面浏览量还是资源网站的资源下载量，大部分都会存在排行榜这个东西。排行榜提供了一个热门信息的入口，也是口碑营销和用户从众心理的典型体现。但对于一个优秀的网站而言，80%以上都不会用自然排名，多少会动一些“小手脚”，那不是在欺骗用户吗？是的，我们有时候确实在做这样的事情。而相比那些金钱驱动的对用户不负责任的更改排名的方式（大家应该都懂的），下面介绍的更改排名的小技巧对用户而言绝对是“美丽的谎言”。

自然排名的弊端

　　先来看看如果网站完全按照自然规则来定制排行榜会出现怎么样的情况：

　　当然可能没有这么夸张，但排行上的内容保持1个月甚至3个月都没有变化还是有可能的。网民的从众心理是不容忽视的，对于一个在网站没有明确目的四处闲逛的用户来说，各类排行榜变成了他们最好的入口；或者我们可以从数据的层面来解释下这个问题，一般排行榜会挂在网站的什么位置？首页，分类索引页，侧边栏？反正是那些用户容易看到，能够轻易点击的地方，这些页面或位置的共同特点就是高曝光，以首页为例，来看看我的博客的曝光排名前5的页面：

　　从数据中可以看到首页的浏览量差不多是其他页面的10倍，所以对于一个资源而言，是否放入排行榜将会导致至少有5倍左右的曝光量的差异，即如果要完成同样的转化目标，未放入排行榜的商品需要比放入排行榜的商品高出4倍的转化率，对于同样的商品，如果放在排行榜只要4%的转化就可以完成100个交易，那么如果把它撤出排行榜同样要完成100个交易就需要高达20%的转化，简直就是天壤之别，这就是排行榜的魔力。

　　这就是所谓的马太效应，是一个非常有趣的现象，但无论对于网站还是用户而言，马太效应的存在都是不利的，网站无法将那些排行之外的有潜力的商品推销出去，而用户同样会看不到那些排行榜之外更有价值的产品。所以我们需要设法去规避马太效应。

如何规避马太效应

　　马太效应（Matthew Effect），简单地说就是“强者愈强，弱者愈弱”。不得不承认马太效应是一个极其强大的自然法则，全世界都在试图规避这个法则，但又有多少能够真正的解决问题的。这个在经济、社会学界让人十分头疼的问题似乎在互联网这个虚拟的领域还是存在许多解决方案的，其中一个在其他领域绝对无法适用的方法就是——随机数。

　　其实在排行榜中规避马太效应的方法有很多，如果网站的数据和运算平台足够强大，完全可以借助一些算法去有效地解决这个问题，之前我也介绍过一个有效的内容推荐方法，或者如果能根据用户行为分析的结果提供根据用户兴趣定制的个性化排行榜，那下面的内容你可能就不必再看下去了。但对于一个小型网站或者刚刚起步数据还不是很全的新产品而言，随机数将会是规避马太效应的一个最简单有效的方法。

　　产生随机数的方法有很多，随机数也有很多不同类型，比如常见的取值范围在(0,1]的两位小数，或者是随机生成1到100的自然数。更改排行榜的方法也有很多，下面就用1-100的自然随机数来例举几个我想到的调整TOP10排行榜的方法：

随机排行方法1

　　调整策略：在前30名内容中随机取10个放入排行榜。

　　实现方式：为前30名的每个内容分配一个随机数，然后根据随机数排序取前10。

　　适用情况：同样适用前50或者前100打乱次序后随机取10，但是无论是前30还是50的内容排名上不能存在太显著的差异，比如热门书籍，可能前30本书的热门度差异并没有那么明显，那么就可以使用这种随机排序法。

随机排行方法2

　　调整策略：将排行榜的8、9、10名替换成11-20、21-30、31-40中各取一个随机内容。

　　实现方式：其实就是生成11-20、21-30、31-40范围的3个随机数，放到排行榜的8、9、10三个位置，先对1-100的随机数做一个简单处理，将其除以10 取余数，于是就相当于是0-9的随机数，在分别加上11、21、31就生成了11-20、21-30、31-40范围的3个随机数，取相应的内容放到排行榜即可。

　　适用情况：存在明显的明星产品，比如软件下载网站的下载前几名会一直被某些软件占据，这些软件确实是用户最常用的软件，跟其他软件的下载量存在显著差距，这个时候就不要去动排名前几的产品，而只要随机变动排名后几位的产品就行。

随机排行方法3

　　调整策略：随机取排行榜中的1个位置来放置推荐的内容。

　　实现方式：有了上面的例子，这个实现起来就比较简单了，其实就是生成一个1-10的随机数，先将1-100的随机数除以10 取余数，再加1即可，再将排行榜上这个随机数的内容替换成推荐内容即可。

　　适用情况：已经有现成的优质内容希望推荐给用户，并能够预期到这些内容很有可能在将来会上排行榜的。

　　好了，上面就是我所列举的几个使用随机数改变排行榜来有效规避马太效应的实际应用，你是不是有更好的想法和方案，在评论中与我分享吧。

关键指标背后的秘密

18 条回复

　　前面的一篇文章介绍了可以用来评估KPI的数据上下文——质量控制图，通常我们会用KPI来衡量一些内容的质量、流量的质量，以及访问的质量等，我们经常根据KPI指标直接排序，并认为排在前几名的就是优质的内容，但其实这种方式并不是对所有的KPI都有效。举个最简单的例子：转化率Conversion Rate是很多网站的KPI指标，一般我们会让为Conversion Rate越高则渠道质量越好，或者内容质量越高，但有一种情况，如果网站内容普遍的转化率为10%，但有一个内容的访问次数一共2次，其中有一次实现了成功的转化，那该内容的转化率就是50%，是不是很“高”？是不是真的有这么高？

　　所以我们在分析关键指标的变化趋势，控制KPI的质量的时候，还需要注意一个问题，那就是如何运用KPI进行有效的评价。

　　其实Google Analytics已经给了我们答案，在前段时间推出了Weighted Sort（赋权排序）的功能，Avinash Kaushik先生在先前的博文——End of Dumb Tables in Web Analytics Tools! Hello: Weighted Sort对这个功能做过介绍，因为近段时间需要用到这个功能，但我的数据并不在GA上，所以我必须自己设计一套给关键指标赋权的体系，以发现到底这些KPI值可以达到多少预期，这里来分享下我的应用实例。

KPI期望值公式

　　还是以转化率Conversion Rate为例，电子商务中每个商品的转化率应该是：购买该商品成功的数量/该商品被浏览的次数，所以从统计学的角度来看，当商品的浏览次数（不妨叫做基数，数学上的集合元素个数或者统计学上的样本总数）这个基数越大时，转化率CR的置信度也就越高，同样是10%的转化率，浏览次数为1000的商品显然要比浏览次数只有100的商品在转化率这个数值上的可信度要高，统计学上称为“大数定理”。

　　根据上面的结论，我们需要根据每个商品转化率的真实值（Actual Value），权衡它的可信度，进而计算得到该商品转化率的期望值（Excepted Value），而这里的可信度就是真实值可以获得的权重，比如60%，那么还有个问题，既然是加权和，另外的40%的权重应该由什么来中和呢？参考GA中Weighted Sort的计算公式，用的是均值，也就是所有转化率的平均，非常不错的idea，于是我们可以得到以下公式了：

期望值（Excepted Value）=权重（Weight）×真实值（Actual Value）+（1-权重）×均值（Average Value）

　　我们看看哪些数据我们现在就可以拿到，权重显然还不行，真实值应该已经统计得到了，均值？既然有了所有的真实值，那么均值就是一个取平均的简单计算了。好的，那下面就说说我是如何来确定这个权重的。

权重的确定

　　先看看权重需要符合哪些原则，应该表现为怎样的一个特征。显然，权重的取值范围应该在[0,1]，也就是0到100%之间；另外，权重跟基数应该是正相关的，也就是基数越大，权重应该越大。如果你看过我之前的文章——数据的标准化，是不是已经想到了什么？是的，里面有几个公式可以直接用，简单地说，就是将基数进行归一化处理。

　　KPI的基数一般都是自然数，比如转化率的浏览次数、Bounce Rate的访问数，人均消费的用户数等，所以反正切函数atan不适用，min-max和log函数都适用，可以用散点图简单看一下分别用这两种方法归一化之后权重和基数的变化关系：

Min-max

　　Min-max是直线的正相关，也就是权重和基数同比例地变化，变化速度一直。

Log函数

　　Log函数是对数曲线的正相关，也就是权重的变化速度要比基数来得快。

　　根据这两个方法的特征，我选择了log函数作为权重的计算函数，因为它更符合基数和可信度之间的关系。

应用实例

　　既然KPI期望值的计算公式，及公式所有需要的数据都已经可以得到了，那么我们就来看看，KPI的基数是如何影响KPI的期望值的：

　　即基数越大，期望值越接近真实值，反之，则越接近平均值。算法和公式确定之后，我们就可以将其应用到实际的案例当中去了，这里以网站的转化率CR为例，看看这个KPI期望值的算法是不是有效的。

渠道	进入访问数	转化访问数	真实转化率	权重	期望转化率
渠道1	1534	118	7.69%	79.81%	7.51%
渠道2	9817	641	6.53%	100.00%	6.53%
渠道3	682	43	6.30%	70.99%	6.45%
渠道4	136	11	8.09%	53.45%	7.49%
渠道5	795	69	8.68%	72.65%	8.17%
总计	12964	882	6.80%

　　表格中的例子是用转化率评价每个渠道流量的质量，比对加权前后的转化率情况，可以看到渠道4由于进入的访问数（基数）较小，所以预期的转化并没有真实值反映的那么好，甚至要差于渠道1；而渠道1因为基数较大，其真实转化率基本能够反映现实情况，渠道2因为基数最大，所以期望值就是实际值。

　　你也不妨试着用上述的方法转化下你的KPI，发掘一下KPI背后到底隐藏着哪些真相，也许你会发现转化后的结果更加可信，更加能让数据需求方所接受了，那么这个转变就成功了。不要忘了在评论中发表下尝试后的感想，分享下你的使用经历。　