T检验和卡方检验

32 条回复

　　好久没有更新博客了，今天更新一篇关于数据分析方法的文章，主要是基于统计学的假设检验的原理，无论是T检验还是卡方检验在现实的工作中都可以被用到，而且结合Excel非常容易上手，基于这类统计学上的显著性检验能够让数据更有说服力。还是保持一贯的原则，先上方法论再上应用实例，这篇文章主要介绍方法，之后会有另外一篇文章来专门介绍实际的应用案例。

关于假设检验

　　假设检验（Hypothesis Testing），或者叫做显著性检验（Significance Testing）是数理统计学中根据一定假设条件由样本推断总体的一种方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。既然以假设为前提，那么在进行检验前需要提出相应的假设：

　　H0：原假设或零假设（null hypothesis），即需要去验证的假设；一般首先认定原假设是正确的，然后根据显著性水平选择是接受还是拒绝原假设。

　　H1：备择假设（alternative hypothesis），一般是原假设的否命题；当原假设被拒绝时，默认接受备择假设。

　　如原假设是假设总体均值μ＝μ₀，则备择假设为总体均值μ≠μ₀，检验的过程就是计算相应的统计量和显著性概率，来验证原假设应该被接受还是拒绝。

T检验

　　T检验（T Test）是最常见的一种假设检验类型，主要验证总体均值间是否存在显著性差异。T检验属于参数假设检验，所以它适用的范围是数值型的数据，在网站分析中可以是访问数、独立访客数、停留时间等，电子商务的订单数、销售额等。T检验还需要符合一个条件——总体符合正态分布。

　　这里不介绍t统计量是怎么计算的，基于t统计量的显著性概率是怎么查询的，其实这些计算工具都可以帮我们完成，如果有兴趣可以查阅统计类书籍，里面都会有相应的介绍。这里介绍的是用Excel的数据分析工具来实现T检验：

　　Excel默认并没有加载“数据分析”工具，所以需要我们自己添加加载项，通过文件—选项—加载项—勾选“分析工具库”来完成添加，之后就可以在“数据”标签的最右方找到数据分析这个按钮了，然后就可以开始做T检验了，这里以最常见的配对样本t检验为例，比较某个电子商务网站在改版前后订单数是否产生了显著性差异，以天为单位，抽样改版前后各10天的数据进行比较：

	改版前订单数	改版后订单数
1	1032	1187
2	1178	1245
3	1098	1379
4	1045	1094
5	976	1173
6	1101	1364
7	1276	1119
8	1215	1268
9	987	1303
10	1065	1274

　　首先建立假设：

H0：μ₁＝μ₂，改版前后每天订单数均值相等；
H1：μ₁≠μ₂，改版前后每天订单数均值不相等。

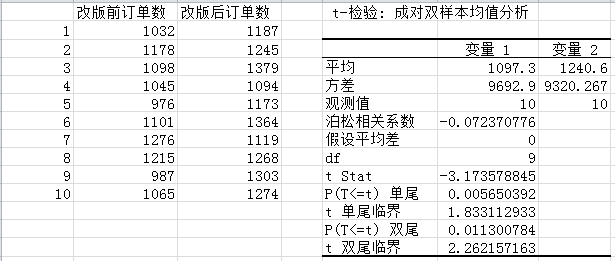
　　将数据输入Excel，使用Excel的数据分析工具，选择“t检验：平均值的成对二样本分析”，输出检验结果：

　　看到右侧显示的结果是不是有点晕了，看上去有点专业，其实也并不难，只要关注一个数值的大小——单尾的P值，这里是0.00565，如果需要验证在95%的置信水平下的显著性，那么0.00565显然小于0.05(1-95%)，拒绝零假设，认为改版前后的订单数存在显著性差异。简单说下为什么选择单尾显著性概率P，而不是双尾，对于大部分网站分析的应用环境，我们一般需要验证改动前后数值是否存在明显提升或下降，所以一般而言只会存在一类可能——或者提升或者下降，所以只要检验单侧的概率即可，就像上面例子中改版后的订单数均值1240.6大于改版前的1097.3，我们需要验证的就是这种“大于”是否是显著的，也就是做的是左侧单边检验，这种情况下只要关注单尾的显著性概率P即可。

卡方检验

　　卡方检验（chi-square test），也就是χ²检验，用来验证两个总体间某个比率之间是否存在显著性差异。卡方检验属于非参数假设检验，适用于布尔型或二项分布数据，基于两个概率间的比较，早期用于生产企业的产品合格率等，在网站分析中可以用于转化率、Bounce Rate等所有比率度量的比较分析，其实在之前的文章——Abandonment Rate的影响因素进行过相关的应用。这里同样不去介绍χ²是如何计算得到的，以及基于χ²统计量的显著性概率的查询等，这里直接以转化率为例来比较网站改版前后转化率是否发生了显著性差异，抽样改版前后各3天的网站分析数据——总访问数和转化的访问数，用“转化访问数/总访问数”计算得到转化率：

	改版前	改版后
总访问数	30567	33651
转化访问数	2976	3698
转化率	9.74%	10.99%

　　首先建立假设：

H0：r₁＝r₂，改版前后转化率相等；
H1：r₁≠r₂，改版前后转化率不相等。

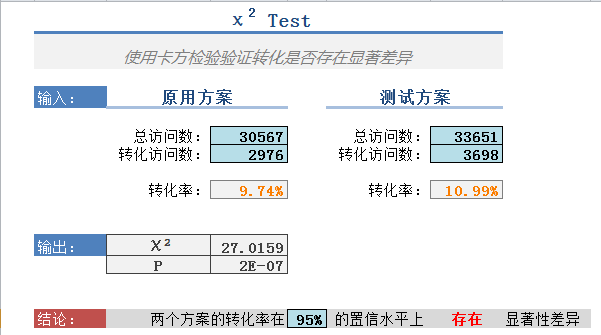
　　其实这是一个最简单的四格卡方检验的例子，也无需使用SPSS（当然你足够熟悉SPSS也可以使用类似的统计分析工具），为了简化中间的计算步骤，我这里用Excel直接制作了一个简单的卡方检验的模板，只要在相应的单元格输入统计数据就能自动显示检验的结果：

点击下载：卡方检验示例

　　Excel中浅蓝色的单元格都支持输入，包括原用方案和测试方案的总访问数和转化访问数，另外置信度95%也是支持修改了，如果你需要99%的置信水平，只要修改这个单元格即可。

　　怎么看检验结果？其实非常简单，只要看那个红色的“存在”单元格的显示结果即可，上面的案例中两者的转化率“存在”显著性差异，如果不存在，则该单元格相应的就会显示“不存在”，有了这个模板对于A/B Testing等类似的数据比较也显得非常简单容易，或者说其实这个Excel模板就是为了A/B Testing而量身定制的。

　　好了，就到这里吧，其实这篇文章并不是想从专业的统计学的角度来介绍T检验和卡方检验，只是想让大家了解这两个方法的原理和适用条件，能够用最简单的方式去使用诸如此类的方法让数据更具说服力，请继续关注之后奉上的应用实例。