在博客之前的文章——优化网站信息架构我曾经提到过关于迷失用户(Lost Visits)的定义,以及如何使用Google Analytics的高级群组(Advanced Segment)去区分出这批用户。最近在看《用户体验度量(Measuring the User Experience)》,发现自己实在太嫩了,人家Smith早在1996年就对迷失度(Lostness)有了定义,同时给出了迷失度L的计算公式,这里借花献佛,分享给大家。
在博客之前的文章——优化网站信息架构我曾经提到过关于迷失用户(Lost Visits)的定义,以及如何使用Google Analytics的高级群组(Advanced Segment)去区分出这批用户。最近在看《用户体验度量(Measuring the User Experience)》,发现自己实在太嫩了,人家Smith早在1996年就对迷失度(Lostness)有了定义,同时给出了迷失度L的计算公式,这里借花献佛,分享给大家。
![]()
即,L = sqrt[ (N/S-1)2 + (R/N-1)2 ]
L:迷失度
N:访问的不同页面数(Unique Pageviews)
S:访问的总页面数(Pageviews)
R:完成任务必需的最小页面数
Smith同时给出了迷失度的评定标准:最佳迷失度为0,迷失度小于0.4时,用户不会显示任何可观察到的迷失特征;迷失度大于0.5时,用户显现迷失特征。
结合公式,我们可以看到这里对迷失度的定义主要考虑到的是:1、重复访问相同的页面,2、没有能够用最简单的方式完成任务,过多地在网站中徘徊。其实第一眼看去这个公式有一定的道理,但细想一下其实也存在着不合理的地方。通常我们需要去获取知识,阅读和总结他人的经验,但如果只是一味地套用书本或者别人的东西,那么你就输了,尤其是在发展如此迅速的互联网领域。那么我们来看看这个公式有何不妥:
我们先思考这样一个问题:迷失的用户会表现怎样的特征?显然,当用户在网站中找不到自己需要的东西的时候会来回地点击各种页面,频繁地返回首页或者索引页面,那么从这个角度看,显然这个公式是成立的,迷失用户的表现特征就是频繁地重复浏览同一页面,并且浏览的页面数会比正常访问多得多。但再换一个角度思考,逆向思考下前面的问题:一个正常的用户会不会出现重复浏览同一页面或者浏览页面数较多的情况?显然也是可能的,简单的例子,如果你对我的博客非常感兴趣,看了一篇文章后还想看另外的文章……于是你来回于博客的文章页面和文章专题推荐或者网站地图页面之间,于是这些列出了文章索引的页面被一次又一次地重复访问着;再如,如果一个用户上电子商务网站的目的不是购物,而是闲逛,看看有没有便宜货,或者只是针对某类商品比对下商品的好坏及价格的差异,以伺机下手,那么这个时候这些用户的访问页面数就会异常的多,但他们其实都没有迷失。所以,上面的公式无法为你从所有的用户中挑出那些迷失的用户,最多只能对已知的迷失用户计算他们的迷失度,哪些是低度迷失,哪些是高度迷失。
 但其实Smith没有错,错的是这个高速发展的时代,这也是我为什么说尤其在互联网领域不要直接照搬一些东西来直接应用于自身的原因。1996年,很明显还处于WEB1.0时代,完全没有现在网站的那些复杂交互和多样的功能,当时的网站大部分做的只是信息的单向发布,而用户访问网站的任务也是单一的,可能就是查找到自己想要的那个信息页面。所以我反而觉得这个迷失度公式在当时绝对是适用的,而且Smith在当时就能总结得出这个的度量公式足见其对如今大热的“用户体验”的先知先觉以及对用户体验度量的智慧。同时这个公式对于当前网站的迷失度衡量也不是完全无效,如果是用户体验的小组在做可用性实验,为实验设定的情景是需要用户在网站中完成一个特定的任务,那么这个公式完全是有效的,所以总结起来就是这个公式对复杂的多任务的网站迷失度衡量无效,而对基于单任务的简单网站或者实验环境是有效的。
但其实Smith没有错,错的是这个高速发展的时代,这也是我为什么说尤其在互联网领域不要直接照搬一些东西来直接应用于自身的原因。1996年,很明显还处于WEB1.0时代,完全没有现在网站的那些复杂交互和多样的功能,当时的网站大部分做的只是信息的单向发布,而用户访问网站的任务也是单一的,可能就是查找到自己想要的那个信息页面。所以我反而觉得这个迷失度公式在当时绝对是适用的,而且Smith在当时就能总结得出这个的度量公式足见其对如今大热的“用户体验”的先知先觉以及对用户体验度量的智慧。同时这个公式对于当前网站的迷失度衡量也不是完全无效,如果是用户体验的小组在做可用性实验,为实验设定的情景是需要用户在网站中完成一个特定的任务,那么这个公式完全是有效的,所以总结起来就是这个公式对复杂的多任务的网站迷失度衡量无效,而对基于单任务的简单网站或者实验环境是有效的。
既然这个公式对于当前的网站大部分时间不适用,我们就需要对其进行改良,使其适用于普遍的网站。再观察下这个公式,我们会发现其实它跟数据挖掘里面的欧几里得距离度量的计算方式十分相似,可以理解为所有的比例为1时是最理想的状态,公式计算的结果就是每个样本点与这个1的理想点的距离,距离越近迷失度越低,距离越远迷失度越高。所以这个思路完全可以借鉴,但显然只考虑浏览页面的这些度量还不够,我们需要加入其他的网站分析度量。
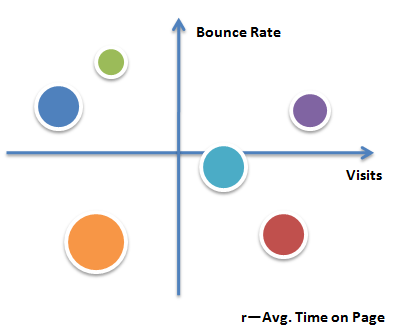
对于现在的大部分网站而言,功能是多样化的,用户使用网站的任务不再是单一的,所以无法为不同任务的用户确定一个统一的完成任务的最小访问页面数,而公式的前半部分依然有效,我们尝试用其他度量来替换后半部分。于是自然而然的想到了停留时间,当用户没有迷失时他们会在自己感兴趣的页面停留一段时间,那么页面平均停留时长(Avg. Time on Page)不会很小,所以改进后的公式如下:
![]()
即,L = sqrt[ (N/S-1)2 + (T/R-1)2 ]
L:迷失度
N:访问的不同页面数(Unique Pageviews)
S:访问的总页面数(Pageviews)
T:访问页面的平均停留时间(Avg. Time on Page)
R:网站正常的页面平均停留时长(既定值)
这个公式同样有几点需要注意,首先N/S和T/R要保证小于等于1,这样迷失度L计算的结果才会落在[0,sqrt(2)]之间,才有评定是否迷失的可行性。N/S可以保证小于等于1,但T/R无法保证,所以再套用公式之前需要做一步数据筛选的工作,也就是过滤那些可以被简单认定不是迷失的访问(建议过滤访问页面数小于3或者页面平均停留时间大于R的所有访问),筛选后的所有访问即是需要去认定是否具有迷失倾向的访问,同时有保证了T/R小于等于1这个规则。至于R的值如何确定,可以先看一下你自己网站的几个数据:
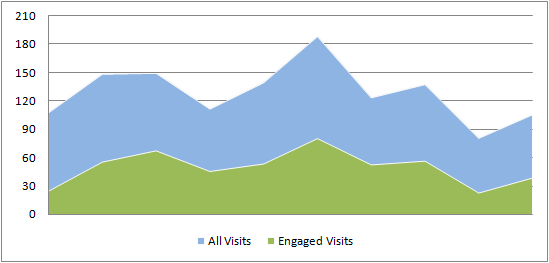
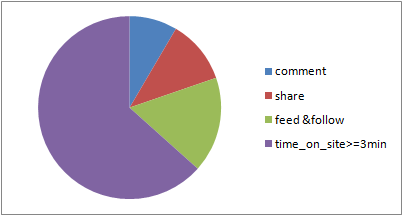
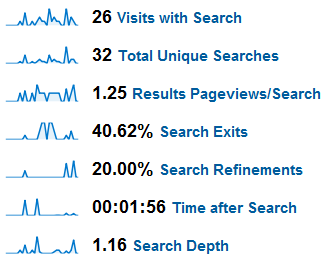
从近一个月的数据观察,我的博客的页面平均停留时间(Avg. Time on Page)为2分钟半左右,所以我暂定公式中的R(网站正常的页面平均停留时长)为2分钟,用高级过滤器查看所有Time on Page小于2分钟的访问大概占到了网站所有访问的45%。同时,上图给出的3个指标恰恰就是公式中需要用到的上需要用到的3个指标,结合刚刚给定的R值,公式中所有需要的变量我们都已经可以拿到了,下面来看看几个示例:
| 序号 | N | S | T | R | L |
| 1 | 4 | 5 | 60 | 120 | 0.5385 |
| 2 | 5 | 8 | 25 | 120 | 0.8760 |
| 3 | 4 | 5 | 20 | 120 | 0.8570 |
上表中计算得到了3个访问样本的迷失度度量L的值,很显然我们当前没法判定到底哪个迷失了哪个没有,所以还缺少一个判定基准(Benchmark),正如上面Smith给出的0.4和0.5,因为公式的变更我们可能需要重新定义这个基准。当然,如果你要用非常严谨科学的态度去定义这个基准线的话,这个过程完全可以作为一个研究课题,进行可用性的实验,观察实验用户的迷失情况,结合每个实验用户的指标数据最终给出一个迷失度的判断基准。当然如果你有兴趣,这个完全可以作为你的毕业设计或者学校科研课题去展开研究,我这边没有时间和资源去完成这个庞大的项目,只能按照经验值进行预估,针对我的博客,我认为当用户的重复访问页面比例超过1/3,并且页面平均停留时间不到30秒时,用户可能已经表现出一定的迷失倾向,将这个数值代入公式得到的迷失度L的值约为0.82,那么这个就可以作为衡量用户迷失的一个基准线,当L大于0.82时用户表现迷失的倾向,小于0.82则为正常访问。
当然我这里提出的迷失度度量公式同样存在优化空间,如果你有更好的想法,可以一起交流,欢迎在评论里面提出你的想法。
可能这篇文章的中间写了一大堆“废话”,主要是自己当时看到这个公式时思考如何将它有效地应用到实际的一个过程,实在没有耐心的朋友可以直接跳过,不影响文章的整体实现思路,不要抱怨:“怎么不早说,现在才提,我看都已经看下来了”,如果你看完了,就证明你有一颗足够淡定的心。其实我自己觉得在获取信息的时候(无论是看书还是看网上的文章)思考过程才是最重要的,这是对信息的一个有效过滤的过程,只有思考之后你获取的信息才是优质的,才是被你真正吸收的。但也有一个弊端,就是发现自己看书实在太慢太拖沓,现在手上正在阅读的有4本书,都是现在进行时,每本书的进度在1/3到1/2不等,涉及数据分析、用户体验、数据挖掘和报表展现,精力不够集中,一段时间不能同时兼顾太多呀,反而拖慢进度。