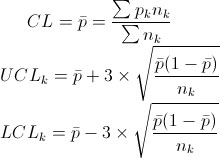标签归档：统计学

网站KPI的质量控制

——数据的上下文2

KPI-Quality-Control 　　前面的一篇文章——时间序列的趋势分析主要介绍的是通过同比和环比的方法为指标设置数据上下文（Context），从而观察和分析各指标在时间序列上的变化趋势，我的建议是在网站的目标指标（Goal）中使用这类方法。所以这篇文章就紧接着上一篇的专题，还是针对内部基准线（Internal Benchmark）的设定，主要解决的是网站关键绩效指标（KPI）的数据上下文的设置，推荐使用的分析工具是——质量控制图。

为什么将质量控制图用于KPI

　　需要明确一个工具可以用于何处，首先必须了解这个工具，所以概念和用处必不可少，这个可以直接参考质量控制图文章中的介绍，这里简单整理出几条适合于使用质量控制图的指标的前提条件：

指标能够体现产品或功能的质量情况；
指标能够持续地被观察测量，并且可以被量化，即从统计角度有足够的样本容量；
在正常情况下，指标的变化趋势保持恒定，不是持续上涨或下降，也不会经常出现大幅波动，即符合正态分布。

　　根据上述的适用条件，应该能够大概明白为什么要用控制图来作为网站KPI的参照设置标准，KPI是衡量网站的质量和表现的指标，在正常情况下，KPI可以保持稳定的趋势，不会出现大幅的波动。这跟网站的目标指标存在差异，一个运营良好的网站，它的目标（如收益）应该是保持稳定增长状态，而不是保持恒定，而它的KPI（如转化率）则应该保持恒定的趋势，除非受到了特定因素的影响或者网站做出了更改和变动。所以KPI指标的特点都符合使用质量控制图的条件。

KPI质量控制图的应用

　　这里选择最常见的两个网站的KPI指标举例下应用的过程，一个是基于网站转化率（Conversion Rate）的P控制图，另一个是基于平均订单价值（Average Order Value, AOV）的X-MR控制图，这里的数据都以天为单位，选择15天的数据进行举例，数据也都是虚拟的。

转化率的P控制图

　　这里以电子商务的交易转化率为例，我们需要获取每天的总访问数和完成交易的访问数，进而相除得到转化率，再根据P控制图的公式计算得到CL、UCL和LCL，为了图表的美观，我选择使用了样本容量取均值，也就是保证UCL和LCL的一致，而不是每天取各自的值，具体的数据见图表，包括15天的数据：

日期	总访问数	成功交易访问数	转化率	CL	UCL	LCL
2010-12-01	10231	201	1.96%	1.81%	2.16%	1.45%
2010-12-02	12874	229	1.78%	1.81%	2.16%	1.45%
2010-12-03	11229	231	2.06%	1.81%	2.16%	1.45%
2010-12-04	9870	201	2.04%	1.81%	2.16%	1.45%
2010-12-05	11804	237	2.01%	1.81%	2.16%	1.45%
2010-12-06	11652	224	1.92%	1.81%	2.16%	1.45%
2010-12-07	13259	236	1.78%	1.81%	2.16%	1.45%
2010-12-08	11891	167	1.40%	1.81%	2.16%	1.45%
2010-12-09	12876	213	1.65%	1.81%	2.16%	1.45%
2010-12-10	14562	240	1.65%	1.81%	2.16%	1.45%
2010-12-11	12933	259	2.00%	1.81%	2.16%	1.45%
2010-12-12	13548	241	1.78%	1.81%	2.16%	1.45%
2010-12-13	15230	256	1.68%	1.81%	2.16%	1.45%
2010-12-14	13815	276	2.00%	1.81%	2.16%	1.45%
2010-12-15	15766	248	1.57%	1.81%	2.16%	1.45%

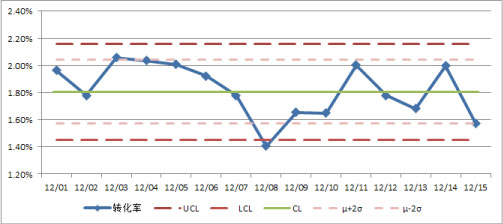
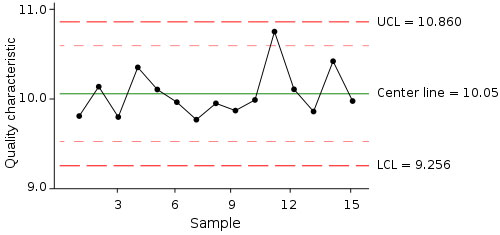
　　根据表中的数据很容易就可以画出相应的P控制图，见下图（添加了μ±2σ的线）：

　　最后就是根据控制图寻找数据可能存在的异常并找到发生异常的原因，根据上图比对控制图的控制规则，可以发现这15天的数据存在2个地方的异常：

12月8日的数据低于LCL，表现异常；
12月3日到12月8日的数据连续6天呈下降趋势，存在异常。

　　到这里，数据层面的工作已经结束了，但接下去这一步却至关重要，就是分析发生异常的原因，这里抓住两个点：从12月3日开始数据呈下降趋势，12月8日到达低谷，之后开始反弹。那么我们可以知道很可能在12月3号的时候网站内部的调整或外部事件导致了数据异常的发生，并且持续到了12月8日，同时通过分析12月8日低谷的细分数据进一步明确到底是哪一块出现了问题，并做出及时的响应和调整，避免类似事件的再次发生。

订单均价的X-MR控制图

　　还是电子商务的KPI——平均订单价值，即所有成交订单的总价值除以订单数，当网站运营的产品没有做出大幅调整时，一般这个指标是保持恒定的，并且因为是均值所以每天之差的波动幅度不会很大，所以可以使用均值-移动极差X-MR控制图。

　　首先要先计算得到每天的平均订单价值，再通过当天与前一天的值相减计算得到移动极差MR，再根据X-MR控制图的公式计算得到CL、UCL、LCL，见下表（也是15天的数据）：

日期	订单均价	MR	X_CL	X_UCL	X_LCL	MR_CL	MR_UCL	MR_LCL
2010-12-01	103.76	12.65	103.48	133.84	73.12	11.41	37.29	0
2010-12-02	129.12	25.36	103.48	133.84	73.12	11.41	37.29	0
2010-12-03	107.30	21.82	103.48	133.84	73.12	11.41	37.29	0
2010-12-04	97.45	9.85	103.48	133.84	73.12	11.41	37.29	0
2010-12-05	105.10	7.65	103.48	133.84	73.12	11.41	37.29	0
2010-12-06	115.78	10.68	103.48	133.84	73.12	11.41	37.29	0
2010-12-07	105.21	10.57	103.48	133.84	73.12	11.41	37.29	0
2010-12-08	98.78	6.43	103.48	133.84	73.12	11.41	37.29	0
2010-12-09	101.74	2.96	103.48	133.84	73.12	11.41	37.29	0
2010-12-10	96.53	5.21	103.48	133.84	73.12	11.41	37.29	0
2010-12-11	97.99	1.46	103.48	133.84	73.12	11.41	37.29	0
2010-12-12	114.20	16.21	103.48	133.84	73.12	11.41	37.29	0
2010-12-13	116.18	1.98	103.48	133.84	73.12	11.41	37.29	0
2010-12-14	80.29	35.89	103.48	133.84	73.12	11.41	37.29	0
2010-12-15	82.76	2.47	103.48	133.84	73.12	11.41	37.29	0

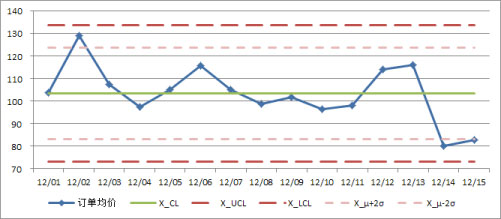
　　X-MR控制图产生两张图，一张是均值X的控制图，另一张是移动极差MR的控制图，先是均值的（也包含了μ±2σ的线）：

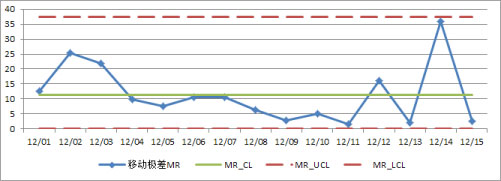
　　再来一张移动极差的控制图：

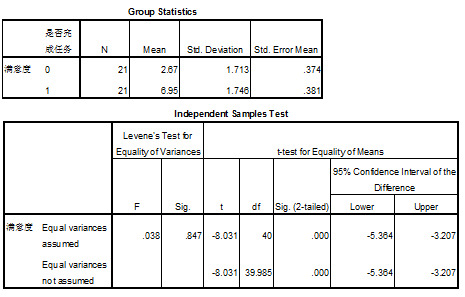
　　同样，还有最重要的一步，就是发现数据的异常和寻找异常发生的原因。首先来看均值控制图，比对控制规则可以发现最近3天中两天的数据都在μ-2σ线以下，这给了我们一个很好的预警信号——数据有变坏的趋势，我们需要去寻找原因并做出快速的响应和调整了；再看移动极差控制图，也有一个异常的规律——连续8个点在中心线以下，为什么？这段时间数据的波动极其平滑，或者相对的说明时间段的两端波动较大，是什么导致了这种异常的波动趋势？这些都需要从业务角度或者外部因素中去寻找原因。所以数据分析师不仅仅是计算和展现数据，更重要的是基于数据的分析，寻找数据背后的影响因素和数据变化的原因。

　　上面就是我的两个应用，对于质量控制图，你是不是还能想到更加有创意的应用方案，欢迎跟我交流评论。这篇文章就作为2010年的收尾，祝大家新年快乐，希望2011能给大家带来更多的新意和惊喜，我的博客也会在新的一年里不断地向大家奉上更加精彩的内容，希望能跟大家一起不断地学习进步。

质量控制图

13 条回复

　　其实之前的一篇文章——网站数据分析的基本流程介绍过质量管理（Quality Management, QM）相关的内容，只是介绍的是概念和流程这类比较定性的东西，这篇文章也是跟质量管理相关的内容，但介绍的主要是定量分析相关的工具——质量控制图。

质量控制图的概念与用处

　　如果要系统地介绍，可能要从质量管理(Quality Management,QM)开始，从传统的质量管理七工具，到全面质量管理阶段的6σ管理，这里不去展开，只介绍质量控制图。

　　质量控制图，简称控制图（Control Chart），是质量管理七工具之一，由美国的贝尔电话实验所的休哈特(W.A.Shewhart)博士在1924年首先提出，因此也称为“休哈特控制图”。最初的应用当然是在生产领域，使用抽样的方式检验产品的质量是否处于控制状态。一般而言，指标的波动受随机因素和系统因素的影响，如果指标只受到随机因素的影响，那么在正常情况下指标的变化状态是稳定的、可控的，但如果发生某种系统性的变化就会使指标超出原先可控的波动范围，处于失控状态，所以控制图就是帮助我们及时发现这种失控状态，从而进行及时的调整。

　　质量控制图通过统计上均值μ和标准差σ的状况来衡量指标是否在稳定状态，同时选择3σ来确定一个正常波动的上下限范围（根据正态分布的结论，指标的特征值落在μ±3σ之间的概率是99.73%），使用均值μ作为控制图的中心线（Center Line, CL），用μ+3σ作为控制上限（Upper Control Limit, UCL），用μ-3σ作为控制下限（Lower Control Limit, LCL），如图。

　　根据衡量的指标数值类型的差异，质量控制图主要分为两类：计数型控制图和计量型控制图，下面分别介绍其中的一种：

质量控制图具体用法

　　因为生产制造业和互联网行业存在着较大差异，所以这里只介绍适合用于网站分析的2个控制图。其中计数型控制图中主要介绍P控制图，主要用于定类型变量，即符合二项分布检验“是否”的变量，如用户是否完成交易、用户是否为新用户……这类指标一般会以比率的形式出现，如转化率、新用户比例等，而P控制图正是衡量这些比率是否出现异常（在生产行业通常用于不合格率等）；另外的计量型控制图主要用于一些关键的数值度量，如每个订单的消费额、每个用户的下载次数等，这类指标在网站分析中通常计算全部数据的均值来观察波动情况，其实计量型控制图最常用的是均值-极差（X-R）和均值-标准差（X-S）控制图，但两者都是通过取样的方式实现的，并且每次取样的样本数最好能保持相等，所以这类抽样统计不太适合于上述网站分析中的指标，这里介绍个相对能够普遍适用并且计算也没有那么复杂的图——单值-移动极差（X-MR）控制图。下面一个个来，先是P控制图：

P控制图

　　根据中心极限定理规律，当二项分布的样本容量足够大时，分布趋向正态N(ρ, ρ(1-ρ)/n)（这里用ρ先暂代下p均值，上横线很难打出来，具体见下面图中公式），所以总体均值μ就是ρ，方差σ²就是ρ(1-ρ)/n，进而就可以计算得到中心线CL、控制上限UCL、控制下限LCL：

p-chart-expression

–p_k：每组样本的比例值，n_k：每组样本容量

　　我在这里使用了UCL_k和LCL_k，也就是每组样本都有各自的控制上限和控制下面，当然我们也可以跟CL一样使用统一的UCL和LCL，这时n不再使用每组的样本容量，而是使用每组样本容量取均值的结果，只是简单的变换，公式就不贴出来了。

X-MR控制图

　　第二类计量型控制图中的单值-移动极差（X-MR）控制图，需要先计算指标的移动极差：MR=|X_i-X_i-1|，即每个数值减去前一个相邻的数据的绝对值，进而计算指标均值和移动极差均值，通过公式转换算出均值X控制图和移动极差MR控制图的CL、UCL、LCL：

x-MR-Chart-expression

–x_i、MR_i：每个个体的数值和计算得到的极差，k：样本个体数，d₂、D₃、D₄：极差到标准差的转化系数，相当于n=2的极差转化系数，所以在这里可以看作是固定值。

　　通过套用上面的公式，可以计算得到相应的CL、UCL、LCL，结合每个特征值就可以画出控制图。因为这篇文章主要基于方法，同时也主要是为下一篇文章作为技术铺垫，所以不具体举例了，具体实例见之后的——网站KPI的质量控制，这里先附上一张维基百科上的质量控制图：

质量控制图的控制规则

　　既然质量控制图是为了帮助我们及时发现指标的不正常状态，那么当我们看到上面的图以后，需要观察和分析是不是存在异常的点或异常的变化趋势，如何定义这些异常，需要有一套控制规则：即样本点出界或者样本点排列异常：

点超出或落在ULC或LCL的界限；（异常）
近期的3个点中的2个点都高于+2σ或都低于-2σ，近期5个点中的4个点都高于+σ或都低于-σ；（有出现异常的趋势）
连续的8个点高于中心线或低于中心线；（有偏向性）
连续的6个点呈上升或者下降趋势；（有明显的偏向趋势）
连续的14个点在中心线上下呈交替状态。（周期性，不稳定）

　　查资料时发现不同的地方对控制规则有不同的定义，我这里参照的是SPSS里面的规则，具体应该可以根据实际的应用环境进行调整。

　　看到这里，你是不是会发现质量控制图其实很有用，结合图比对这些规则后能够很快地发现指标的异常和可能产生的异常，一目了然。具体应用会在近几天内一并奉上，请继续关注。

提升用户满意度

9 条回复

——让用户更容易地找到需要的信息5

　　在前一篇文章——用户任务完成度分析中我似乎遗漏了一个重要的问题：为什么要分析用户的任务完成度？其实每个网站分析的方案和模型都应该具备它的目的和意义，否者就失去了分析的价值。所以这篇文章就是为了回答这个问题，同时也作为“让用户更容易地找到需要的信息”专题的完结篇。

　　所以这里先提出一个假设：让用户更容易地找到需要的信息进而帮助用户完成预期的任务，能够有效地提升用户满意度。

用户满意度的影响因素

　　我们不妨先来看一下用户满意度是怎么定义的，根据美国顾客满意度指数模型（ACSI, American Customer Satisfaction Index）的描述，用户满意度是用户对产品或服务的预期与实际接受的产品或服务的感受间的差距，差距越小，满意度越高。对于以信息服务为主的网站而言，用户访问网站的预期就是找到自己需要的信息，完成既定的任务（寻找信息、购物、娱乐等），那么如何衡量用户实际接受到的网站服务的质量水平，进而推测它们之间存在的差距？对于用户对网站实际的感受，可以从以下3方面体现：

用户是否完成预期任务（网站是否及格）
完成任务过程中良好的体验（也许网站能打八九十分了）
感受创意或意外的收获（获得附加分的机会）

　　所以，保证用户完成预期的任务是网站质量的及格线，也可以看作是网站的生命线。那么任务完成度对于用户满意度是否有这么重要的影响呢？我们需要对以上的假设进行验证。

任务完成度与用户满意度

　　为了验证任务完成度是否对用户的满意度有显著的影响，我们在统计用户任务完成情况的同时，需要收集用户对网站的满意度，所以上篇文章问卷调查中对用户满意度的打分题中采集到的数据就有了用武之地。我们可以通过比较完成任务的用户与未完成任务的用户对满意度的打分是否存在显著性差异的方法来验证任务完成度对用户满意度的影响是否显著。

　　这里可以使用两组独立样本T检验的方法，把问卷调查中采集到的样本数据分为两组，一组是未完成任务的用户的满意度打分，另一组是完成任务用户的满意度打分，我们可以认为这两组数据都是近似的符合正态分布，进而比较这两组样本的总体均值是否存在显著差异。（或许你认为这个结果是显而易见的，这个验证完全是多此一举，那就当我是画蛇添足，无聊打发时间吧。）

　　首先提出零假设：

H₀： μ₁= μ₂

　　再将收集到的样本数据通过SPSS或Excel的数据分析功能进行双样本均值T检验，过程就不详细论述了，不然估计很多用户立马会离开网站甚至直接关闭浏览器了。

　　从SPSS的分析结果中可以看出，完成任务与未完成任务用户的满意度打分均值（上面一张表Mean值）可以看出，完成用户的满意度均值明显大于未完成用户。从下面那张表的95%置信区间的检验结果可以看到，F检验的显著性概率为0.847>0.05，所以我们可以认为完成任务用户与未完成任务用户的满意度打分的样本方差没有明显差异；而T检验的显著性（双尾）概率近似于0，小于0.05，因此拒绝零假设，即两个样本的总体均值存在显著差异，进而我们可以得出完成任务的用户满意度显著地高于未完成任务的用户满意度。

　　通过上面的分析，我们验证了文章一开始提出的假设，即用户的任务完成度对提升用户的整体满意度有显著的影响。那么如何通过提高用户的任务完成度来提升用户满意度呢？

如何提升用户满意度

　　提升用户满意度，我们可能需要做很多事情，从全局到细节，需要处处为用户的体验和感受着想。既然我们已经验证用户的任务完成度对用户满意度会产生显著影响，那么我们可以先从提升用户的任务完成度开始。这里可以参考我之前写的关于如何让用户更容易地找到需要的信息的4篇文章——优化网站信息架构，优化网站内部搜索，优化网站导航设计，优化相关内容推荐。

　　这些优化可以从普遍的层面上提高用户的任务完成度，但显然以上这些还是不够的，因为用户的知识构成存在着差异，用户遇到的问题也会各不相同，所以上篇文章的问卷中当用户未完成任务时填写的为什么没有完成任务的开放性问题就能发挥作用了，我们需要针对各类用户（甚至个别用户）遇到的不同问题分别提供有效的解决方案，这也是为什么很多网站都会设置FAQ甚至在线客服的原因。

　　所以我们首先要满足用户访问网站的最基本的期望——完成他们预期的任务，从该层面上提升用户满意度，下面是我画的一个简单的示意图，就作为文章的结尾吧：

Abandonment Rate的影响因素

17 条回复

　　前几天看到了Sidney写的一篇文章——电子商务(B2C)网站的Abandonment Rate，里面详细介绍的B2C网站中购物车及付款流程可能造成交易的中断，客户放弃购买该商品的情况，也就是Abandonment Rate。文章中提到了Abandonment Rate可能涉及的影响因素，及如何降低Abandonment Rate的一些方法，感觉对提高电子商务网站商品的销售转化率十分有效。其中谈到Abandonment Rate与商品的价格或商品的销售组合之间可能存在某种联系，为了求证这类联系是否存在，我们可以使用一些定量分析的方法对可能影响Abandonment Rate的某些因素进行了分析。

哪些因素影响了Abandonment Rate

　　一般B2C电子商务网站都会基于商品进行分类，如下图：

　　以卓越销售的商品为例，卓越销售商品以图书音像为主、电子日用品为辅，其下的产品分为图书音像、消费电子、日用消费品等类目，之下还有子类目的划分，最底层就是其销售的商品，如图书Web Analytics 2.0、某品牌的手表等，那么可以整理得到如下的商品列表：

商品类目1	商品类目2	商品类目3	……
商品1	商品3	商品4
商品2		商品5
……		……

　　根据上面的表格，我们可以通过横向对比和纵向对比的方法对Abandonment Rate影响因素进行分析。因为不同的商品类目可能在商品的品牌口碑、本质特征、展示方式、购物车流程等方面存在差异，通过横向比较商品类目的Abandonment Rate是否存在显著性差异，可以确定这么因素的影响情况；而同一类目中商品的纵向对比，可以在控制商品的品牌口碑、本质特征、商品展示方式、购物车流程相似的条件下，比较商品的关注度、价格、购买数量、促销等因素的影响情况。

不同商品类目间的横向比较

　　样本数据的选择：为了说明差异是有商品类目的不同说引起的，我们需要选择商品受关注程度、平均价格、销售情况、促销频率等较为相近的2个商品大类（如鼠标和帽子），以排除这些因素的影响。同时选取合适的时间跨度，你可以选择一个月、一个季度或者任意的时间区间来分析该时间段内样本数据特征。如：

categories-AR-compare

　　样本数据是关于某时间发生频数的统计，所以比较两组样本间的差异可以选择四格表卡方检验的方法，这里的检验结果χ²=16.84，显著性水平p<0.01, 差异有高度统计学意义，拒绝零假设，认为两组数据存在显著性差异。

同一类目中不同商品的纵向比较

　　样本数据的选择：同样我们需要选择关注度、价格、销售数量、促销频率等存在一定差异的相同类目下的商品（如不同品牌、价格和款式的手表）来进行比较分析。同样选取合适的数据时间段，如统计得到以下数据：

商品	关注度	价格	销售数量	促销比率	Abandonment Rate
1	3258	588	251	0.16	0.4487
2	1569	998	76	0.05	0.4711
3	2965	158	206	0.20	0.2639
4	236	2568	15	0	0.5714
5	985	1128	3	0	0.3843

　　我们可以通过excel的数据分析功能获取各列间的相关系数r，首先可以根据r值的正负确定是正相关还是负相关，然后比对以下的相关系数与相关程度的对照表，确定相关性的强弱：

\|r\|>0.95	\|r\|>=0.8	0.5<=\|r\|<0.8	0.3<=\|r\|<0.5	\|r\|<0.3
显著性相关	高度相关	中度相关	低度相关	不相关

　　那么根据结果可以得出以下结论：Abandonment Rate与价格高度正相关，与促销频率中度负相关，与关注度中度负相关，与销售数量低度负相关。

如何降低Abandonment Rate

　　既然已经知道有这些因素影响了B2C的Abandonment Rate，那么我们如何通过网站优化来降低Abandonment Rate呢？其实Sidney在他的文章中已经提到的许多解决的方法是十分有效的，下面根据以上影响因素分析的结果分各因素来简要阐述下我们可以做些什么？

商品类目间的差异

　　如果通过比较分析得出2个或多个商品类目间存在显著的差异，那么首先要确定这个差异是不是由于商品本质特征的不同会导致，因为商品的某些本质特征有时并不是能够人为控制的，诸如：

商品的品牌口碑：网购的用户可能会偏向品牌型产品；
规格的固定性：电子商品的规格确定性会高于衣物等日用品，所以鼠标的Abandonment Rate会低于帽子也不奇怪；
售后服务：一般商品的售后服务由厂商提供，那么这个因素一般是电子商务网站无法控制的。

　　由于以上原因造成的Abandonment Rate偏低的商品类目，网站方面可能就力不从心了，然而如果差异是由一下因素造成的，那么网站就得找找自己的原因的：

商品展示方式的差异：布局、图片、商品描述、一些有误导性的信息……这些也会造成Abandonment Rate的偏高；
购物车流程的差异化：用户可能在购买鞋子时因为需要填写尺码、颜色等信息而直接关闭浏览器离开了，但在购买图书是可能就不会出现这种情况；
用户购买体验：如果网站提供了用户的交流平台，那么客服人员对某类商品的不熟悉或不耐烦也会造成该商品的Abandonment Rate过高。

商品个体因素的影响

　　对于单个商品而言，关注度、价格、销售量、促销频率这些因素可能就决定了Abandonment Rate，但是麻烦来了，以上的这些因素可能很难做持续的改进，这时我们可以采取互补的方式，即通过提高某些有利因素来降低某些不利因素的影响。

　　比如我们发现A产品由于价格过高而造成与同类商品相比Abandonment Rate偏高，而分析证明促销对于降低该类商品的Abandonment Rate有显著的有效性，那么我们可以是增加A产品的促销频率；或者提高关注度对降低Abandonment Rate有效，那么可以把A产品放到网站更加显眼的位置……

　　当然，由于电子商务网站商业模式上的差异，对Abandonment Rate的影响因素可能各不相同，上面也只是举例说明了一部分因素。所以，最好根据自己网站的特点来选取可能的影响因素进行分析，方法可以借鉴上面的两种，如果你有更好地分析方法，欢迎跟我分享。

数据的标准化

53 条回复

　　数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

　　其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上，常见的数据归一化的方法有：

min-max标准化(Min-max normalization)

　　也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下：

　　其中max为样本数据的最大值，min为样本数据的最小值。这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

log函数转换

　　通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

　　看了下网上很多介绍都是x^*=log₁₀(x)，其实是有问题的，这个结果并非一定落到[0,1]区间上，应该还要除以log₁₀(max)，max为样本数据最大值，并且所有的数据都要大于等于1。

atan函数转换

　　用反正切函数也可以实现数据的归一化：

　　使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上。

　　而并非所有数据标准化的结果都映射到[0,1]区间上，其中最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法：

z-score 标准化(zero-mean normalization)

　　也叫标准差标准化，经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：

　　其中μ为所有样本数据的均值，σ为所有样本数据的标准差。