标签归档：统计学

大数定律与抽样陷阱

6 条回复

law-of-large-numbers　　前面一篇文章——难以解释的数据异常——发出来之后，朋友推荐我去读《黑天鹅》，刚刚翻完这本书，发现书中的很多观点和细节的表述都能给人启发，尤其是“叙述谬论”和“过度解释”这个两点能对难以解释的数据异常这篇文章中描述的内容给出另一个侧面的解释。从作者塔勒布的后记和书中表述的观点来看，读过这本书的人可能很容易走入两种认识的极端：

　　1、既然一些未知的黑天鹅事件可能对我们造成极大的影响，那我们就应该去努力预测这些未知事件，以便做好充分的准备来应对这些事件。但作者在书中明确说了黑天鹅事件的不可预测性；
　　2、既然我们无法预测未知，并且未知事件可能对我们的生活造成翻天覆地的影响，我们只能不去做任何的预测和准备，等待命运的审判。但书的副标题是“如何应对不可预知的未来”，所以作者塔勒布并不认为我们什么都做不了，至少能够认识到黑天鹅的存在，打破传统思维的局限性，谨慎地预防，黑天鹅是未知的未知，我们需要为已知的世界和已知的未知做好准备。

　　《黑天鹅》中多次提到大数定律可能会愚弄我们，作为数理统计和概率论中两个经典的理论（中心极限定理和大数定律）之一，为什么遇到黑天鹅事件时就会失效？或者说大数定律在遇到任何的小概率事件时都有可能“失效”，需要谨慎地认识，以防掉入应用中的陷阱。

大数定律

　　大数定律（Law of Large Numbers），指在随机试验中，每次出现的结果不同，但是大量重复试验出现的结果的平均值却几乎总是接近于某个确定的值。典型的例子就是抛硬币的伯努利试验，当抛硬币的次数足够多的时候，正反面出现的概率都接近于1/2。

　　常用的大数定律有伯努利大数定律和辛钦大数定律。其中伯努利大数定律指在n次独立试验中，事件A发生的频率为p，当n足够大时，p无限接近事件A真实的发生概率，即频率的稳定性；辛钦大数定律指若n个独立同分布的随机变量存在数学期望，则当n越大时，其算法平均数越接近于这些随机变量的真实数学期望值，即均值的稳定性。

　　大数定律为统计推断提供了充分的理论依据，我们可以通过抽样的方法用样本统计量的特征去估计总体的特征，而不需要去研究整个总体。当样本的数量越大时，其对总体的估计就越接近总体的真实特征。但在面对小概率事件时，大数定律对总体的估计会显得无能为力，很多时候结论是失效的。

小概率事件

　　假设我们进行重复10000次的伯努利试验，事件A、B、C发生的次数均满足二项分布X~B(n, p)，n代表试验次数，p代表事件发生的概率。其中事件A发生的概率为10%、事件B发生的概率为1%、事件C发生的概率为0.1%。我们知道，满足二项分布的随机变量的均值是np，方差为np(1-p)，于是就可以用变异系数CV（具体内容参见衡量数据的离散程度这篇文章）来衡量这3个事件发生次数的变异性或者波动情况，可以得到如下的结果：

事件 试验次数 发生概率 均值 方差 变异系数
A 10000 10% 1000 900 3.00%
B 10000 1% 100 99 9.95%
C 10000 0.1% 10 9.99 31.60%

　　从上表中可以看出，当试验的次数保持恒定时，事件发生的概率越低，则事件发生的次数会存在越大的波动性或者波动幅度，如果我们继续降低事件发生概率，比如事件D发生概率为0.01%，也就是10000次试验中发生的期望次数是1次，那么事件D的CV就高达99.99%，完全无法预判其是否发生。所以在相同的条件下，小概率事件一定比普遍发生的事件存在更大的变数，概率越小波动的幅度就越大。

抽样误差

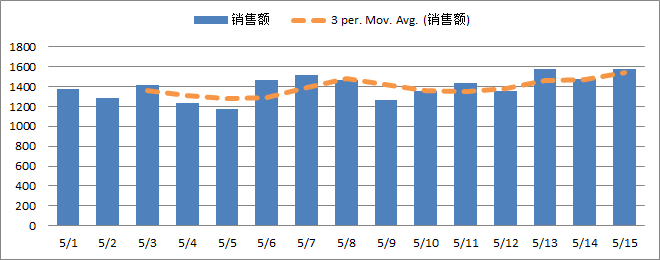
data-sampling　　随着网站数据量的不断增大，数据的处理和统计需要更高的成本，于是有些分析就会借助抽样的方法来处理数据，Google Analytics的免费版当数据量达到上限时就会采用抽样的方式显示结果报表。其实很多时候我们都在使用抽样的方法分析数据，我们可能会用最近7天的数据来评估近段时间的流量变化、转化情况等，但7天并不能完全代表近段时间，其实做的也是一种抽样。下面来看看现实的网站数据分析的例子：

　　转化率（Conversion Rate）是网站分析中非常重要的一个指标，很多公司会把转化率当做运营产品部门的KPI，但对于很多网站而言，转化率并不大，一般不会超过10%（根据网站业务特征的差异和对目标转化的定义不同，转化率在不同网站间没有一个恒定的标准，也不具备可比性），如果网站的内容质量不高或者用户体验不好，转化率也很可能低于1%。这个时候如果用抽样的方法来预估网站整体的转化情况，就很容易掉入抽样误差的陷阱。

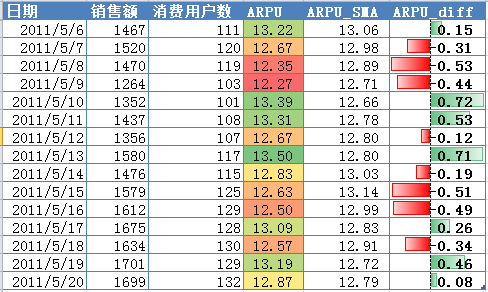
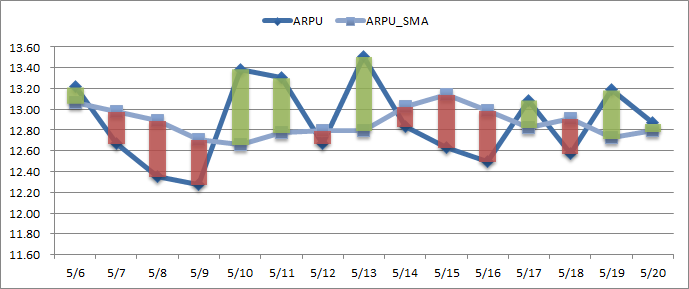
　　网站的转化情况其实是一个二项分布，即转化或未转化，满足X~(n, p)。根据中心极限定理，二项分布的极限是正态分布，一般认为当np和n(1-p)同时大于10时，二项分布近似地满足X~N(np, np(1-p))的正态分布，即均值为np，方差为np(1-p)。将二项分布除以n之后可以得到均值，即概率p的分布，当n大于30时，近似服从N(p, p(1-p)/n)的正态分布，即均值为p，方差为p(1-p)/n，当n无限大时，样本概率p与总体概率就不存在误差，也就是满足大数定律。假如我们从网站每天几百万次的访问中抽样1万次访问来预估整体的转化率，当样本的转化率（即概率p）分别为10%、1%、0.1%时，预估的总体转化率的变异系数同上表，分别为3.00%、9.95%、31.60%（可以用均值为p，标准差为sqrt(p(1-p)/n)进行验证），所以样本转化率越低，使用样本转化率去预估总体转化率就会越不准确。

　　既然过小的转化率在抽样中可能导致预估的结果存在巨大的误差，那么如何合理地选择样本数量来控制这个误差？上面已经提到，当二项分布的np和n(1-p)同时大于10时，可以认为近似满足正态分布，在正态分布下面，就可以计算在一定置信水平下的置信区间（详细计算方法见参数估计与置信区间中的区间估计），而要让抽样的误差控制在可接受的范围内，可以增加抽样的样本数来提升样本对总体估计的可信度。

　　假设我们将置信水平设定在90%（一般认为95%的置信水平是满足统计学意义的，但互联网的数据影响因素较多，普遍波动较大，不需要科研实验那么高的精确度，所以90%的置信水平足够了），即Zα/2取到1.65，我们对转化率的控制一般要求较高，假设在90%的置信水平下，样本的置信区间必须控制在样本转化率的±10%，可以看下在这种条件下各种转化率水平所需的抽样样本数必须满足怎么样的条件：

转化率 10%的转化率 σ需要满足 n需要满足
10% 0.01 <0.00606 >2451
5% 0.005 <0.00303 >5174
1% 0.001 <0.000606 >26958
0.1% 0.0001 <0.0000606 >272032

　　上表的样本数条件可以作为我们抽样时的参考，具体的应用可以根据概率的大小和对置信水平、置信区间的需要进行计算得到。

　　最后再回到黑天鹅，通过上面对小概率事件和抽样误差的解释，其实已经很明显了。黑天鹅是极小概率事件，可能几十年几百年才遇到一次，而大数定律是一个理想化的状态，也就是n值趋近于无穷，我们很难在人生短短数十年经历很多小概率事件，或者我们的知识阅历的储备无法包含这么多的异常，很多事情在几十年的“抽样样本”中是不存在的；同时因为时代在快速地变化，当前可能发生的事件可能仅限于当前这个环境，我们无法通过历史去预见未来。于是我们完全没法知道黑天鹅事件发生的可能性，甚至不知道它的存在，即黑天鹅事件是未知的，也是无法预测的。

　　春节前的最后一篇文章了，提前祝大家春节快乐，一起期待下一年的精彩！ :D

衡量数据的离散程度

8 条回复

　　我们通常使用均值、中位数、众数等统计量来反映数据的集中趋势，但这些统计量无法完全反应数据的特征，即使均值相等的数据集也存在无限种分布的可能，所以需要结合数据的离散程度。常用的可以反映数据离散程度的统计量如下：

极差（Range）

　　极差也叫全距，指数据集中的最大值与最小值之差：

Range

　　极差计算比较简单，能从一定程度上反映数据集的离散情况，但因为最大值和最小值都取的是极端，而没有考虑中间其他数据项，因此往往会受异常点的影响不能真实反映数据的离散情况。

四分位距（interquartile range，IQR）

　　我们通常使用箱形图来表现一个数据集的分布特征：

box-plot

　　一般中间矩形箱的上下两边分别为数据集的上四分位数（75%，Q3）和下四分位数（25%，Q1），中间的横线代表数据集的中位数（50%，Media，Q2），四分位距是使用Q3减去Q1计算得到：

 interquartile-range

　　如果将数据集升序排列，即处于数据集3/4位置的数值减去1/4位置的数值。四分位距规避了数据集中存在异常大或者异常小的数值影响极差对离散程度的判断，但四分位距还是单纯的两个数值相减，并没有考虑其他数值的情况，所以也无法比较完整地表现数据集的整体离散情况。

方差（Variance）

　　方差使用均值作为参照系，考虑了数据集中所有数值相对均值的偏离情况，并使用平方的方式进行求和取平均，避免正负数的相互抵消：

Variance

　　方差是最常用的衡量数据离散情况的统计量。

标准差（Standard Deviation）

　　方差得到的数值偏差均值取平方后的算术平均数，为了能够得到一个跟数据集中的数值同样数量级的统计量，于是就有了标准差，标准差就是对方差取开方后得到的：

Standard-Deviation

　　基于均值和标准差就可以大致明确数据集的中心及数值在中心周围的波动情况，也可以计算正态总体的置信区间等统计量。

平均差（Mean Deviation）

　　方差用取平方的方式消除数值偏差的正负，平均差用绝对值的方式消除偏差的正负性。平均差可以用均值作为参考系，也可以用中位数，这里使用均值：

Mean-Deviation

　　平均差相对标准差而言，更不易受极端值的影响，因为标准差是通过方差的平方计算而来的，但是平均差用的是绝对值，其实是一个逻辑判断的过程而并非直接计算的过程，所以标准差的计算过程更加简单直接。

变异系数（Coefficient of Variation，CV）

　　上面介绍的方差、标准差和平均差等都是数值的绝对量，无法规避数值度量单位的影响，所以这些统计量往往需要结合均值、中位数才能有效评定数据集的离散情况。比如同样是标准差是10的数据集，对于一个数值量级较大的数据集来说可能反映的波动是较小的，但是对于数值量级较小的数据集来说波动也可能是巨大的。

　　变异系数就是为了修正这个弊端，使用标准差除以均值得到的一个相对量来反映数据集的变异情况或者离散程度：

Coefficient-of-Variation

　　变异系数的优势就在于作为一个无量纲量，可以比较度量单位不同的数据集之间的离散程度的差异；缺陷也是明显的，就是无法反应真实的绝对数值水平，同时对于均值是0的数据集无能为力。

　　其实这篇文章只是对基础的统计知识的整理，可以从很多资料里面找到，很多统计学的书里面都是在“统计描述”章节中介绍这些基础的统计量，跟均值、中位数、众数等一起罗列，很少通过统计量的具体应用进行分类，而国外的一些书对知识点的介绍更多的是从实际应用的角度出发的，这里推荐《深入浅出统计学》这本书，虽然介绍的都是基础的统计知识，但可读性比较强，通俗易通，相比国内的一些统计学教程，更容易在大脑中建立起有效的知识索引，在具体应用中能够更加得心应手。

难以解释的数据异常

11 条回复

anomaly　　在分析数据的时候，总有那些一些数据异常无法找到适当的理由进行合理解释，也许可以换个角度来看待这些异常。为什么明明数据发生较大的起伏波动，我们绞尽脑汁还是无法找到合理的原因，这些到底是怎么样的异常，是不是存在一些共性，或者这些异常是不是我们平常所说的异常，抑或是应该归到其他类别，不妨先叫它们“难以解释的异常”。

　　近段时间在读《思考，快与慢》这本书，作者卡尼曼的观点似乎可以给我们一些答案。卡尼曼是心理学和决策学方面的大师，他告诉我们如何避开大脑思考的误区，从而更加理性地进行认知和决策。这里引述书中提及的与上面“难以解释的异常”这个问题相关的两个观点：

  • 回归均值效应：事物会经历好坏的随机波动，但最终会回归到平均水平。
  • 用因果关系解释随机事件：人们总是试图为一些变化寻找可以解释的原因。

迪马特奥和贝尼特斯

　　对于回归均值效应（Mean reversion），卡尼曼举了一些与体育相关的例子，确实这个现象在体育竞技中较为常见：高尔夫球手为什么第二天无法打出前一天的好成绩，球员为什么第二个赛季无法复制前一个赛季的辉煌……这让我联想到了近期切尔西的换帅事件。

　　其实迪马特奥和贝尼特斯之间存在一些有趣的共同点：1) 都是欧冠的冠军教头，2) 能力都没有被完全认可。如果说迪马特奥是没有足够的时间来证明自己的执教能力情有可原的话，那么贝尼特斯显然是自己的选择造成了外界对其能力的质疑。

Di-Matteo-and-Benitez　　迪马特奥在上赛季中后段从助理教练接手切尔西，并以看守主教练的身份一路过关斩将，最终夺取欧冠冠军，成功带回球队历史上第一座大耳朵杯足够让其能在赛季末被扶正，但因为缺乏执教经验始终无法让挑剔的老板对其有足够的信任，于是当球迷和俱乐部还沉浸在上赛季欧冠的荣耀光环下，而球队的表现却无法延续“应有”的辉煌时，迪马特奥下课的命运是注定的。在竞争如此激烈的英超联赛，切尔西无法摆脱回归效应，如果说上个赛季切尔西在诸多有利因素的共同作用，再加上一些运气成分的基础上成功加冕欧冠的话，那么这个赛季这些有利因素不再集中地作用于他们，而他们的运气也似乎“用完了”，成绩回归之前的平均水平实属正常现象，而在昔日光环下的球迷和俱乐部显然认为这是“异常事件”，于是迪马特奥成为了回归效应的受害者。

　　其实这类事件在足球界屡见不鲜，世界杯的98法国，02五星巴西，06意大利都难逃回归效应，夺冠之后成绩下滑，而很多教练也在夺冠之后纷纷辞职，因为他们也明白再续辉煌（摆脱回归效应）是如此之难，斯科拉里、里皮等都做出了明智的选择，而这些冠军球队的替任教练又往往是命运最为坎坷的，毕竟能像博斯克这样让西班牙不断延续辉煌的教练真的不多，而贝尼特斯恰恰当了回悲催的替任者。

　　2010年贝尼特斯接替穆里尼奥成为三冠王国际米兰的主教练，三冠王的光环太过耀眼，而阵容老化加引援不利，注定让国米走上回归效应的道路，于是赛季不到半程，贝帅即被解雇。其实贝尼特斯之前执教生涯的战绩并不是太差，成名于疯狂的“伊斯坦布尔之夜”，但也正是因为这传奇一战成了一座无法逾越的丰碑，即使之后帮助利物浦夺得诸多赛事的冠亚军，也无法让俱乐部和球迷真正的满意，而贝帅的决策失误在于其没有在任何一个辉煌或几近辉煌（07年虽然被米兰复仇雅典，但至少也是个欧冠亚军）的时刻选择退出，直到最后利物浦战绩实在看不下去了才以失败者的身份离开。贝帅真的应该向老辣的银狐里皮或者狡猾的穆里尼奥学习下什么叫做功成身退。

　　而这次，贝帅又一次选择了欧冠冠军光环下的切尔西，尽管这个光环已渐渐褪去，我们也只能祝他好运了。

倒塌的桥梁与突然安静的教室

resonant-bridge　　共振（Resonance）催生了宇宙大爆炸，形成了星辰日月和世间万物，共振现象是自然界最普遍的现象之一。一群士兵骑马通过法国昂热市的某座桥时，共振现象导致了桥梁的倒塌，这个例子被引入初中物理教科书，从而成为了我们认识共振原理的启蒙记忆。但是什么原因引发了共振，进而发生桥梁倒塌这类异常事件，正常情况下同样一群士兵同样行军通过同样的桥，可能几万次中才会出现一次桥梁倒塌，士兵是普通的士兵，桥是正常的桥，产生共振完全是一个随机事件，但正是因为这类事件概率太小，所以人们总是试图从士兵或者桥的身上找原因（但是有时候确实是因为桥存在问题 ;- ) ）。

　　然后是一个在知乎上看到的问题：为什么原来大家都在讨论，声音嘈杂的教室会突然安静下来？这个也许大家都遇到过，也是一个类似的小概率事件，教室里每个人都在断断续续地说话，正常情况下声音的大小总是保持在一个水平波动，但可能突然有一个时刻同时说话的人数减少了，声音也随机地波动到了一个最低点，这个时候大家就会认为是不是发生了什么事情，老师来了？于是纷纷不说话，教室突然鸦雀无声，一片寂静。大家都感觉到了教室声音的“异常”，而试图为这个异常寻找可能的原因。

什么造成了这些“异常”

　　首先来看回归均值效应，一般表现为事物在某段时间表现得非常好，之后回归到正常水平的一个过程。这个按理来说是一个正常的过程，因为事物在诸多因素的共同影响下总有一些随机的波动，关键在于人们总是希望好的状态能够延续，而当事物从一个极好的状态出现下滑时，因为落差较大，所以很容易把回归均值之后的状态当做一种“异常”。如下图：

mean-reversion

　　A段的曲线即使有上下波动，但一般不会被认为有异常，但C段曲线很容易被误认为是异常，因为我们很容易将C段与B段进行比较，而不是A段的均值水平（绿线所示，C段与A段均值差异并不大）。因为这里给出了完整的曲线变化趋势，所以犯这种错误的可能性会降低，但当我们比较短时间内的数据变化，或者简单看数据同环比的时候，就很容易误把回归均值当做一种异常。所以分析数据要结合长期趋势，当事物状态未发生质变而数据明显上升一个台阶的情况下，不要认为好的数据表现总能够持续，因为好的数据表现也只是一个正常的随机波动引起的。

　　解释了回归均值效应，还需要搞清楚的是虽然事物大部分时间都有小幅的随机波动，但偶然也会出现较大的波动，即极好或者极差的状态，正如上图的B段状态，我们如何认定这个状态也是随机的，而不是异常呢，不能因为难以解释而不把过大的数据波动当做一种异常来看？

　　这个问题还是可以从物理学的角度开始解释，先看下波的叠加原理（Superposition Principle）：

Interference-of-two_waves

　　左图的下面2个波在叠加之后合成了更大的振幅，而右图的下面2个波相互干涉，合成后振幅消减为零。引申到数据变化的情境下，一般一个指标会受到多个因素的影响，比如网站的访问量会受多个渠道数据波动的影响，搜索引擎、外部链接、社交媒介、付费广告等这些外部渠道带来的流量总是在变化的，如下图：

factors-superposition

　　当某个渠道的流量异常的时候，如A线所示，或者由于外界因素的影响，如春节或节假日所有渠道的流量都可能普遍下降，如B线所示，这些都可能导致总体访问量的异常，这些异常是可以解释的。C线中每个渠道的数据都未出现明显异常，但由于多个渠道的流量因为随机波动碰巧同时都到了一个较低的点，这个时候总体访问量也会出现明显低于正常水平的情况，于是就出现了“难以解释的异常”。

　　所以，这些“难以解释的异常”之谜可以揭晓了，当很多因素同时作用于某个指标的时候，即使所有的影响因素都没有出现显著的异常，指标数据仍然可能表现异常，虽然这个概率非常低，但确实会发生，这是因为多个因素共同作用下的叠加效应导致的，如果通过细分指标的影响因素没有发现明显的异常，那么不要试图为这个“难以解释的异常”寻找看上去可以解释的原因。

分析的前提—数据质量1

5 条回复

data-profiling　　数据质量（Data Quality）是数据分析结论有效性和准确性的基础也是最重要的前提和保障。数据质量保证（Data Quality Assurance）是数据仓库架构中的重要环节，也是ETL的重要组成部分。

　　我们通常通过数据清洗（Data cleansing）来过滤脏数据，保证底层数据的有效性和准确性，数据清洗一般是数据进入数据仓库的前置环节，一般来说数据一旦进入数据仓库，那么必须保证这些数据都是有效的，上层的统计聚合都会以这批数据作为基础数据集，上层不会再去做任何的校验和过滤，同时使用稳定的底层基础数据集也是为了保证所有上层的汇总和多维聚合的结果是严格一致的。但当前我们在构建数据仓库的时候一般不会把所有的数据清洗步骤放在入库之前，一般会把部分数据清洗的工作放在入库以后来执行，主要由于数据仓库对数据处理方面有自身的优势，部分的清洗工作在仓库中进行会更加的简单高效，而且只要数据清洗发生在数据的统计和聚合之前，我们仍然可以保证使用的是清洗之后保留在数据仓库的最终“干净”的基础数据。

　　前段时间刚好跟同事讨论数据质量保证的问题，之前做数据仓库相关工作的时候也接触过相关的内容，所以这里准备系统地整理一下。之前构建数据仓库基于Oracle，所以选择的是Oracle提供的数据仓库构建工具——OWB（Oracle Warehouse Builder），里面提供了比较完整的保证数据质量的操作流程，主要包括三块：

  1. Data Profiling
  2. Data Auditing
  3. Data Correcting

Data Profiling

　　Data Profiling，其实目前还没找到非常恰当的翻译，Oracle里面用的是“数据概要分析”，但其实“Profiling”这个词用概要分析无法体现它的意境，看过美剧Criminal Minds（犯罪心理）的同学应该都知道FBI的犯罪行为分析小组（BAU）每集都会对罪犯做一个Criminal Profiling，以分析罪犯的身份背景、行为模式、心理状态等，所以Profiling更多的是一个剖析的过程。维基百科对Data Profiling的解释如下：

Data profiling is the process of examining the data available in an existing data source and collecting statistics and information about that data.

　　这里我们看到Data Profiling需要一个收集统计信息的过程（这也是犯罪心理中Garcia干的活），那么如何让获取数据的统计信息呢？

　　熟悉数据库的同学应该知道数据库会对每张表做Analyze，一方面是为了让优化器可以选择合适的执行计划，另一方面对于一些查询可以直接使用分析得到的统计信息返回结果，比如COUNT(*)。这个其实就是简单的Data Profiling，Oracle数据仓库构建工具OWB中提供的Data Profiling的统计信息更加全面，针对建立Data Profile的表中的每个字段都有完整的统计信息，包括：

　　记录数、最大值、最小值、最大长度、最小长度、唯一值个数、NULL值个数、平均数和中位数，另外OWB还提供了six-sigma值，取值1-6，越高数据质量越好，当six-sigma的值为7的时候可以认为数据质量近乎是完美的。同时针对字段的唯一值，统计信息中给出了每个唯一值的分布频率，这个对发现一些异常数据是非常有用的，后面会详细介绍。

　　看到上面这些Data Profile的统计信息，我们可能会联想到统计学上面的统计描述，统计学上会使用一些统计量来描述一些数据集或者样本集的特征，如果我们没有类似OWB的这类ETL工具，我们同样可以借助统计学的这些知识来对数据进行简单的Profiling，这里不得不提一个非常实用的图表工具——箱形图（Box plot），也叫箱线图、盒状图。我们可以尝试用箱形图来表现数据的分布特征：

box-plot

　　箱线图有很多种表现形式，上面图中的是比较常见的一种箱线图。一般中间矩形箱的上下两边分别为数据集的上四分位数（75%，Q3）和下四分位数（25%，Q1），中间的横线代表数据集的中位数（50%，Media，Q2），同时有些箱线图会用“+”来表示数据集的均值。箱形的上下分别延伸出两条线，这两条线的末端（也叫“触须”）一般是距离箱形1.5个IQR（Q3-Q1，即箱形的长度），所以上端的触须应该是Q3+1.5IQR，下端的触须是Q1-1.5IQR；如果数据集的最小值大于Q1-1.5IQR，我们就会使用最小值替换Q1-1.5IQR作为下方延伸线末端，同样如果最大值小于Q3+1.5IQR，用最大值作为上方延伸线的末端，如果最大或者最小值超出了Q1-1.5IQR到Q3+1.5IQR这个范围，我们将这些超出的数据称为离群点（Outlier），在图中打印出来，即图中在上方触须之外的点。另外，有时候我们也会使用基于数据集的标准差σ，选择上下3σ的范围，或者使用置信水平为95%的置信区间来确定上下边界的末端值。

　　其实箱线图没有展现数据集的全貌，但通过对数据集几个关键统计量的图形化表现，可以让我们看清数据的整体分布和离散情况。

　　既然我们通过Data profiling已经可以得到如上的数据统计信息，那么如何利用这些统计信息来审核数据的质量，发现数据可能存在的异常和问题，并对数据进行有效的修正，或者清洗，进而得到“干净”的数据，这些内容就放到下一篇文章吧。

Google Website Optimizer报告解读

7 条回复

google-website-optimizer　　前段时间用博客的几个测试页面尝试了下使用Google Website Optimizer做A/B测试，经过这段时间收集了一些测试数据，感谢大家帮忙点击。其实之前一直想介绍Google的这个网站对比实验优化工具，完全免费而且操作简单，并且在不久的将来独立的Google Website Optimizer就会消失，这块功能会被整合到Google Analytics里面，相信很多GA的用户已经在Content模块中发现了新增的Experiments这个功能，这个就是从Google Website Optimizer衍生而来，功能和使用上面应该会有些调整和变化。

　　对于Google Website Optimizer的使用其实并没有那么复杂，使用实验的创建向导结合网页的提示和帮助，普通的用户创建自己的实验完全没有问题，只是网站的千差万别可能有很多的细节方面需要注意，或者需要想一些办法让实验过程和监控结果更加有效。所以这里不介绍GWO工具使用本身，我比较感兴趣的其实是实验输出的结果报表，里面涉及对结果的区间预估，测试方案胜出的概率，提升幅度等，这些指标都用统计学的方法计算得到，相比直接比较两组观察值，比较结果更加科学，更具说服力。

　　首先看下GWO输出的报告，这里用的是A/B测试，如果使用Multivariate Testing（MVT）报告会有细微的差异，但指标及统计逻辑应该是相同的：

GWO-Report

　　我用GWO实现了一个最简单的A/B测试，一个原始版本和一个测试版本，输出的报告主要是比较实验过程中设定的转化率。上方的折线图显示的是原始版本和实验版本的转化率趋势，截至目前的转化情况显示在下方表格的最右侧（Conv./Visitors），从指标名称看，GWO衡量转化率用的是转化的用户数，应该使用Cookie来唯一识别用户（这里仅是在博客新建了几个简单测试页面，所以数据量较小，而转化率相比正常网站都明显偏高）。

　　所以，这里重点研究了下图中表格红框内的3个指标，看它们是如何计算得到的。

估算转化率

　　从图中红框1中可以看到Est. conv. rate，GWO报表对目前得到的转化率做了正负区间的预估，进而可以得到目前该版本转化率可能的置信区间（详见前一篇文章——参数估计与置信区间），这里用当前的转化率估计该版本的总体转化率p，进而可以计算得到总体标准差σ= sqrt(p(1-p)/n)，比如这里原始版本的总体标准差约为0.0540，而测试版本的标准差约为0.0647，根据Zα/2×σ计算得到的上表中正负的7.6%和9.1%，所以我们就可以猜出GWO用的Zα/2大概为1.4，这个数值我在测试期间接连验证过几次，基本非常稳定，根据Z值表，这个置信区间大概的置信度在84%，也不知道为什么GWO要选择这么个置信度。

　　红框1的上方我们可以看到GWO根据测试的效果将测试版本分成了三类，分别用绿色表示胜出的测试版本，黄色表示不确定的测试版本，红色表示落败的测试版本。Google仅给出了简单的说明，建议我们可以选择使用显示为绿色的版本，因为它们有很大的可能性（也只是可能）优于原始版本，而显示红色版本建议可以停止测试。具体到指标需要达到怎样的水平才会显示绿色或红色，我没有去验证，有使用经验的或者感兴趣的同学可以去观察下试试。

胜过原始版本的几率

　　之前在T检验和卡方检验这篇文章介绍过可以使用卡方检验的方法来比较二项分布数据间的概率是否存在显著差异，但卡方检验只能检验差异的显著性，没法直接说明某组样本的概率有多少的几率超过另外一个样本，所以在GWO的报告里面没有使用卡方检验，而使用了单尾Z检验。当样本数量超过30的时候，我们一般会使用Z检验来替代T检验比较两组独立或配对样本间的均值差异，因为这里只是为了证明一组样本概率明显超过另外一组样本的可能性，所以使用了单尾检验。计算Z统计量的公式如下：

Z-Test

　　根据表格的数据，原始方案和测试方案的转化率均值p分别为78.9%和78.0%，根据公式S2=p(1-p)分别计算两组样本的方差为0.1665和0.1716，而两组样本数n分别为57和41，进而计算得到Z=0.1068，查Z值表可得Z=0.10的概率为46.02%，Z=0.11的概率为45.62%，表中显示的Chance to Beat Orig.=45.9%，介于两者之间，使用的应该是类似的统计方法得到的值，偏差是因为中间精度处理引起的。

观察到的改进

　　图中红框3的Observed improvement，这个指标需要结合红框1的转化率置信区间来看，结合条形图可以比较清晰地得出结果，看下我用Excel画的展现估算转化率的类似条形图：

GWO-est-conv-rate

　　这里我用了两条辅助的虚线，如果第一个是原始版本，那么测试版本所有与原始版本转化率预估区间的差异都会用颜色展现，而观察到的改进就是着色区间的转化率差异。比如图中第二个条形的红色区间展现的相应值为-4.2%，而第三个应该是-1.6%+0.6%=-1.0%，即左侧的负值区间加上右侧的正值区间，第四个为2.9%。这样GWO报表中所有指标的计算都可以明确了 :)

　　其实，大部分时候我们使用工具来完成分析或测试的过程，也不一定非要了解所有指标最底层的计算逻辑，我们只要知道这些指标的含义及作用，在分析具体问题时合理地使用这些指标就可以。而有些时候我们只能统计得到一些基础数据，所以如何使用这些基础数据得到一些有价值有说服力的分析结论就需要用到一些合适的统计学方法，这也是这篇文章去解读GWO输出报表的原因。

参数估计与置信区间

4 条回复

confidence-level 

　　我们总是希望能够从一些样本数据中去探究数据总体的表现特征，在网站数据分析中也是如此，我们试图从最近几天的数据表现来推测目前网站的整体形势是怎么样的，有没有变好或者变差的信号，但当前几天的数据无法完全代表总体，所以这里只能使用“估计”。同时，网站的数据始终存在波动，将最近时间段的数据作为抽样样本很可能数据正好处于较低或者较高水平，所以我们用样本得到的估计值不可能是无偏差的，我们同时需要去评估这个估计值可能的变化区间。 

　　参数估计（Parameter Estimation）是指用样本的统计量去估计总体参数的方法，包括点估计和区间估计。 

点估计

　　点估计（Point Estimation）是用抽样得到的样本统计指标作为总体某个未知参数特征值的估计，是一种统计推断方法。 

　　一般对总体参数的估计会包括两类：一种是用样本均值去估计总体均值，对应到网站数据中的数值型指标，比如网站每天的UV，我们可以用近一周的日均UV去估计目前网站每天唯一访客数量的大体情况；另外一种是用样本概率去估计总体概率，对应到网站数据中的比率型指标，比如网站的目标转化率，我们可以用近3天的转化率去预估网站当天目标转化的水平；同时我们会计算样本的标准差来说明样本均值或者概率的波动幅度的大小，从而估计总体数据的波动情况。 

　　点估计还包括了使用最小二乘法对线性回归做曲线参数的拟合，以及最大似然估计的方法计算样本集分布的概率密度函数的参数。 

区间估计

　　区间估计（Interval Estimation）是依据抽取的样本，根据一定的正确度与精确度的要求，估算总体的未知参数可能的取值区间。区间估计一般是在一个既定的置信水平下计算得到总体均值或者总体概率的置信区间（Confidence Interval），一般会根据样本的个数和标准差估算得到总体的标准误差，根据点估计中用样本均值或样本概率估计总体均值或总体概率，进而得出一个取值的上下临界点。 

　　我们可以将样本标准差记作S，如果我们抽样获取的有n个样本，那么总体的标准差σ就可以用样本标准差估算得到： 

std_dev-to-std_err 

　　从这个公式中我们可以看到大数定理的作用，当样本个数n越大时，总体指标差σ越小，样本估计值越接近总体的真实值。Excel的图表里面也提供了添加“误差线”的功能： 

Excel-error-bars 

　　有了总体的标准差σ，我们就可以使用区间估计的方法计算总体参数在一定置信水平下的置信区间，置信区间（Confidence Interval）给出了一个总体参数的真实值在一定的概率下会落在怎么样的取值区间，而总体参数落在这个区间的可信程度的这个概率就是置信水平（Confidence Level）。当抽取的样本数量足够大时（一般n>30），根据“中心极限定理”，我们可以认为样本均值近似地服从正态分布。 

　　根据Z统计量的计算公式： 

Z-Score 

　　假如在1-α的置信水平下，则总体均值μ的置信区间为： 

Confidence-Interval 

　　这里样本均值和标准差都可以根据抽样的结果计算得到，所以在既定置信水平的条件下，我们只要查Z值表（Z-Score）得到相应的Z值就可以计算得到总体均值的置信区间。对于置信水平或者叫置信度的选择，在统计学中一般认为95%的置信度的结果具有统计学意义，但其实在互联网领域数据的分析中不需要这么高的置信度，我们有时也会选择80%或者90%的置信度，相应的Z值见下表： 

置信水平1-α 对应Z值Zα/2
95% 1.96
90% 1.65
80% 1.28

　　对于总体概率的估计，在具备足够样本数量的条件下，我们用样本概率p预估总体概率，而总体概率的标准差则是sqrt(p(1-p)/n)，同样可以计算得到置信区间。 

　　其实这篇文章的内容大部分都可以在统计学书籍或者网上Wiki里面找到，当然写到博客里面不是为了做科普，这里的每篇“数据分析方法”类目下的文章都是跟相应的网站数据分析的应用文章结合，这篇也不例外，如果你对相关内容感兴趣，请关注后续发布的文章，或者订阅我的博客吧。

比较测试的设定和分析

24 条回复

——数据的上下文5

Controlled-Trial　　基于前一篇文章——T检验和卡方检验中提出的数据比较方法，其实我们在生物或者化学的实验中经常也会涉及比较，这篇文章就来具体介绍如何在现实的网站分析环境中使用这些方法，使用的前提和环境是怎样的。

　　其实我们在做数据分析的时候经常进行比较分析，但往往以观察分析法为主，“T检验和卡方检验”为我们的比较分析提供了很好的科学的定量分析方法，让比较的结果更有置信度和说服力。但在使用定量分析的比较方法前，还有很多因素需要考虑，当我们需要精确地分析比较的效果，我们一般都会做比较测试，而其中涉及测试环境的设定，数据的选择和获取等，以排除一些非相关因素的干扰，让比较的结果更加真实可信，所以下面就介绍下如何合理地进行比较测试。

比较测试的类型

　　比较测试或实验的类型有很多，但都跳不出抽样、重复、分组、比较这几个流程，所以从实验设计的角度，我们可以简单地把比较测试分为两类：基于时间序列的组内比较和基于对照实验的组间比较。

时间序列的组内比较

　　基于时间序列的组内比较一般在时间序列上的某个时间点引入实验变量或者施加实验刺激，并在实验刺激的前后进行重复测试，分别叫做“前测”和“后测”，对前测和后测分别进行抽样比较，从比较的结果反映实验刺激是否对结果有显著的影响。详细的流程见下图：

Time-Serial-Comparison

　　举个有趣的例子，如果公司的员工前4个月在正常的薪资待遇的水平上工作，体现出正常的工作效益和工作满意度；然后从第5月开始给员工进行加薪（施加实验刺激），再观察之后4个月员工的工作效益和工作满意度，将之前4个月的结果（前测）与后4个月的结果（后测）进行比较，分析员工的工作效益和工作满意度是否存在显著性差异，进而证明加薪这个实验刺激是否对提升员工的工作效益和满意度有显著性影响。这就是简单的时间序列比较测试的基本流程。

　　但基于时间序列的比较测试会受很多因素的干扰，比如上面的例子在实验过程中CPI的增长、公司业绩的下滑或者运营环境的恶化都可能导致实验结果的失效，或者验证的结果不可信，所以下面会具体说明需要排除的干扰因素。

对照实验的组间比较

　　基于时间序列的组内比较只是基于一组样本，只是样本在时间序列的某个点上受到了实验变量的刺激；而对照实验需要设定两组样本，也就是“实验组”和“控制组”，并对实验组施加实验刺激，控制组维持原状态不变，从而比较实验组和控制组是否存在显著差异来反映实验的刺激是否影响了结果。因为对照实验涉及两组样本，所以这里需要额外注意抽样的规范性，我们需要保证两组样本的特征具有相似性，可以进行比较。具体的实验设计见下图：

Controlled-Trial-Comparison

　　还是使用上面的例子，但在对照实验中设置对照组和实验组是必需的，比较不再是基于前测和后测。比如我们让部分员工维持当前的薪资待遇继续工作，而另外一部分的员工提升他们的薪资待遇，从而比较为提升待遇的员工和提升待遇的员工的工作效益和工作满意度的差异，如果差异显著就可以证明提升薪资待遇这个实验刺激对结果是有显著影响的。

　　对照实验因为参与比较的两组样本都是基于相同的时间序列轴，所以随着时间变化的影响因素对实验的比较结果的影响不再重要，因为两组样本同时受到了同样的影响，但因为是组间比较，所以两组样本如果存在差异性，那么对结果就会造成较大影响，比如上例中A组选择的是基层员工，B组选择中高层员工的话，比较的结果显然是缺乏科学性的。下面就具体介绍下比较测试中可能存在的影响因素有哪些？

前提与影响因素

　　首先看一下从用户体验的角度，如果我们进行可用性实验，需要考虑的影响因素有哪些：

  • 外部噪声和干扰：外部干扰信息、临时的电话和呼唤等；
  • 经验和熟练：因为可用性实验一般需要重复过程，所以随着实验的进程，用户渐渐熟悉对网站和工具的使用；
  • 消耗：随着实验进程，用户可能失去耐心，或者精力无法集中；
  • 主观预测：当进行重复实验时，用户容易用先前的测试结果来推测之后的测试，同样会影响实验结果的可信度。

　　以上是可用性实验中需要考虑的影响因素，有些只存在于实验环境中，如果衍生到WEB分析中，同样需要注意一些影响因素，而对于上面介绍的时间序列组内比较和对照实验组间比较，各自的影响因素又各不相同：

时间序列的组内比较

　　基于时间序列的组内比较可能存在的干扰因素相对较多，因为外部环境和内部环境都会随着时间发生变化，所以为了让基于时间序列的前测和后测两组数据具有可比性，我们必须规避以下几类因素的影响：

  • 数据本身存在的自然增长或下降趋势；
  • 规避节假日或者外部事件的影响；
  • 规避特殊的营销推广其带来的影响；
  • 规避内部其他可能影响测试结果的因素（实验刺激必须唯一）。

对照实验的组间比较

　　对照实验因为两组样本处在相同的环境和时间序列上，所以需要规避的影响因素比上面要少很多，但相较组内比较，组间比较需要额外考虑两组样本是否具有可比性：

  • 两组样本特征相似，可比较（抽样规范性）；
  • 实验组跟对照组之间只存在唯一的实验刺激导致的差异。

　　无论是基于时间序列的组内比较还是基于对照实验的组间比较，都要规避外部环境的重大变动，或者特殊的外部事件对网站造成的重大影响，或者服务器故障或数据统计异常造成的数据不完整或不准确，因为这些因素造成的影响已经可能导致用于比较的数据本身就存在巨大误差，或者不可信，都是无法规避和弥补的。

网站应用实例

　　网站环境下最常见的比较测试显然就是A/B Testing，AB测试为网站的改版和优化提供了对照实验的比较测试环境，具体的流程如下：

A-B-Testing

　　访问网站的用户被AB测试的系统自动分成了两组，一般情况下是按比例对半划分，当然很多情况下也会根据需要按其他合适的比例，如1:3，1:5等。这里的A方案和B方案一个是未做改动的原方案，另一个是改版后的新方案，如果一次需要测试多个改进方案的效果，那么就需要设定多个实验组，而控制组只要一个就行。

　　A/B Testing属于对照实验的组间比较的测试方法，所以同样需要符合对照实验的前提，规避对照实验可能存在的其他影响因素。因为A/B Testing遵循了简单随机抽样的方法，所以我们可以认为实验组和对照组之间的样本无明显的差异，具有可比性。同时，对照实验基于相同的内外部环境和相同的时间序列，所以诸如节假日、数据自然增长或下降、特殊推广期等的影响可以不用考虑，但某些特别重大的外部事件或者网站服务器故障导致的数据问题还是需要在比较测试之前进行排除。另外对照实验中必须控制每个实验组的实验刺激只能是1个，不然无法区分到底是哪个实验刺激对实验结果造成的影响。

　　在规避上述影响因素后，基于A/B Testing的数据比较可以使用我在上篇文章中介绍的“T检验和卡方检验”的方法直接进行显著性的检验，进而验证实验刺激对结果是否存在显著性影响，这里不再重复举例了。

　　A/B Testing有自己的优势，它比基于时间序列的比较的限制因素要少很多，但A/B Testing毕竟需要预先构建相应的自动分流系统，可能在某些特定的环境下或者对某些特殊的网站而言没有相应的环境可以进行AB测试，这个时候我们就不得不选择时间序列的比较测试。

　　基于时间序列的组内比较需要规避推广、节假日和外部营销事件的影响，这个可以通过选择合理的测试起止时间，选择合适的前测和后测样本进行规避，但如果网站本身数据存在明显的上涨或下降趋势，那么我们必须对数据进行必要的处理：

改版前 改版后
用户数 订单数 用户数 订单数
12395 576 13920 704
13237 641 14391 715
13450 732 15692 781
13872 693 16533 839
14673 770 15916 813

　　上表是某电子商务网站基于时间序列改版前后的比较测试，前测和后测各选取5天的数据进行比较，以“订单数”作为比较指标，为了说明改版能不能显著地提升每天订单的数据。如果我们不考虑数据本身的自然增长，直接比较改版前后日均订单数的差异：

　　改版前日均订单数682.4 < 改版后日均订单数770.4

　　显然改版后日均订单有显著提升，说明改版有效？那么我们将数据的自然增长考虑进去，我们可以将日均用户数的增长率作为整个网站数据的自然增长率：

　　(改版后日均用户数 – 改版前日均用户数) / 改版前日均用户数 = 13.05%

　　改版前日均订单数682.4 * 1.13 = 771.1 > 改版后日均订单数770.4

　　比较的结果发生了改变，改版前的日均订单数在乘上自然增长率后要比改版后的日均订单数高，但相差不多，从结果看应该是改版对订单数的提升无显著影响。显然后面考虑网站自然增长率后的比较结果更加科学，更加可信和具有说服力。这就是我们在基于时间序列的比较测试中需要考虑的一些问题。当然上面是基于简单的观察分析比较，如果需要更具统计学意义的定量比较，同样可以对数据进行自然增长处理后使用T检验或者卡方检验。

　　这篇文章可能写得有点长，本来想分两篇发布，但因为内容不太好分段，也怕影响内容的连贯性，所以最终都整合到了一篇，希望大家有耐心能够看完。当然期间的一些看法如果有问题，或者大家有自己的其他见解，都可以在下面评论留言，非常欢迎大家提出其他的看法。一边在看羽毛球世锦赛男单决赛一边更新了这篇博客，希望文中不要存在过多地错误或者错别字 ;)

T检验和卡方检验

32 条回复

　　好久没有更新博客了，今天更新一篇关于数据分析方法的文章，主要是基于统计学的假设检验的原理，无论是T检验还是卡方检验在现实的工作中都可以被用到，而且结合Excel非常容易上手，基于这类统计学上的显著性检验能够让数据更有说服力。还是保持一贯的原则，先上方法论再上应用实例，这篇文章主要介绍方法，之后会有另外一篇文章来专门介绍实际的应用案例。

关于假设检验

　　假设检验（Hypothesis Testing），或者叫做显著性检验（Significance Testing）是数理统计学中根据一定假设条件由样本推断总体的一种方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。既然以假设为前提，那么在进行检验前需要提出相应的假设：

　　H0：原假设或零假设（null hypothesis），即需要去验证的假设；一般首先认定原假设是正确的，然后根据显著性水平选择是接受还是拒绝原假设。

　　H1：备择假设（alternative hypothesis），一般是原假设的否命题；当原假设被拒绝时，默认接受备择假设。

　　如原假设是假设总体均值μ＝μ0，则备择假设为总体均值μ≠μ0，检验的过程就是计算相应的统计量和显著性概率，来验证原假设应该被接受还是拒绝。

T检验

　　T检验（T Test）是最常见的一种假设检验类型，主要验证总体均值间是否存在显著性差异。T检验属于参数假设检验，所以它适用的范围是数值型的数据，在网站分析中可以是访问数、独立访客数、停留时间等，电子商务的订单数、销售额等。T检验还需要符合一个条件——总体符合正态分布。

　　这里不介绍t统计量是怎么计算的，基于t统计量的显著性概率是怎么查询的，其实这些计算工具都可以帮我们完成，如果有兴趣可以查阅统计类书籍，里面都会有相应的介绍。这里介绍的是用Excel的数据分析工具来实现T检验：

　　Excel默认并没有加载“数据分析”工具，所以需要我们自己添加加载项，通过文件—选项—加载项—勾选“分析工具库”来完成添加，之后就可以在“数据”标签的最右方找到数据分析这个按钮了，然后就可以开始做T检验了，这里以最常见的配对样本t检验为例，比较某个电子商务网站在改版前后订单数是否产生了显著性差异，以天为单位，抽样改版前后各10天的数据进行比较：

  改版前订单数 改版后订单数
1 1032 1187
2 1178 1245
3 1098 1379
4 1045 1094
5 976 1173
6 1101 1364
7 1276 1119
8 1215 1268
9 987 1303
10 1065 1274

　　首先建立假设：

H0：μ1＝μ2，改版前后每天订单数均值相等；
H1：μ1≠μ2，改版前后每天订单数均值不相等。

　　将数据输入Excel，使用Excel的数据分析工具，选择“t检验：平均值的成对二样本分析”，输出检验结果：

t-test-sample

　　看到右侧显示的结果是不是有点晕了，看上去有点专业，其实也并不难，只要关注一个数值的大小——单尾的P值，这里是0.00565，如果需要验证在95%的置信水平下的显著性，那么0.00565显然小于0.05(1-95%)，拒绝零假设，认为改版前后的订单数存在显著性差异。简单说下为什么选择单尾显著性概率P，而不是双尾，对于大部分网站分析的应用环境，我们一般需要验证改动前后数值是否存在明显提升或下降，所以一般而言只会存在一类可能——或者提升或者下降，所以只要检验单侧的概率即可，就像上面例子中改版后的订单数均值1240.6大于改版前的1097.3，我们需要验证的就是这种“大于”是否是显著的，也就是做的是左侧单边检验，这种情况下只要关注单尾的显著性概率P即可。

卡方检验

　　卡方检验（chi-square test），也就是χ2检验，用来验证两个总体间某个比率之间是否存在显著性差异。卡方检验属于非参数假设检验，适用于布尔型或二项分布数据，基于两个概率间的比较，早期用于生产企业的产品合格率等，在网站分析中可以用于转化率、Bounce Rate等所有比率度量的比较分析，其实在之前的文章——Abandonment Rate的影响因素进行过相关的应用。这里同样不去介绍χ2是如何计算得到的，以及基于χ2统计量的显著性概率的查询等，这里直接以转化率为例来比较网站改版前后转化率是否发生了显著性差异，抽样改版前后各3天的网站分析数据——总访问数和转化的访问数，用“转化访问数/总访问数”计算得到转化率：

  改版前 改版后
总访问数 30567 33651
转化访问数 2976 3698
转化率 9.74% 10.99%

　　首先建立假设：

H0：r1＝r2，改版前后转化率相等；
H1：r1≠r2，改版前后转化率不相等。

　　其实这是一个最简单的四格卡方检验的例子，也无需使用SPSS（当然你足够熟悉SPSS也可以使用类似的统计分析工具），为了简化中间的计算步骤，我这里用Excel直接制作了一个简单的卡方检验的模板，只要在相应的单元格输入统计数据就能自动显示检验的结果：

chi-square-test-sample

点击下载：卡方检验示例

　　Excel中浅蓝色的单元格都支持输入，包括原用方案和测试方案的总访问数和转化访问数，另外置信度95%也是支持修改了，如果你需要99%的置信水平，只要修改这个单元格即可。

　　怎么看检验结果？其实非常简单，只要看那个红色的“存在”单元格的显示结果即可，上面的案例中两者的转化率“存在”显著性差异，如果不存在，则该单元格相应的就会显示“不存在”，有了这个模板对于A/B Testing等类似的数据比较也显得非常简单容易，或者说其实这个Excel模板就是为了A/B Testing而量身定制的。 ;)

　　好了，就到这里吧，其实这篇文章并不是想从专业的统计学的角度来介绍T检验和卡方检验，只是想让大家了解这两个方法的原理和适用条件，能够用最简单的方式去使用诸如此类的方法让数据更具说服力，请继续关注之后奉上的应用实例。

指标的移动平均

6 条回复

——数据的上下文3

Moving-average　　接着之前数据上下文（Context）的话题继续探讨网站分析中可以设立的数据意境。数据上下文2中的网站质量控制图为网站的KPI指标给出了有效的监控体系，但质量控制图毕竟比较严谨，其实对于大部分互联网环境的指标而言，可能并不符合这么苛刻的条件，于是我们需要寻找另外的方法来监控和观察这些指标的变化趋势。

　　同样是基于时间序列的分析，前面的文章——时间序列的趋势分析中主要介绍了“同比”和“环比”的概念，这里在介绍一种方法——移动平均法。其实移动平均线应用最多的是在股市，5日、10日、30日均线都是用移动平均法计算得到的；而移动平均线也是Excel中的趋势线的一种类型。所以移动平均法最常见的用法就是对于趋势变化的观察分析，但同时也具备了预测和比较监控的功能。下面介绍两个最简单常用的移动平均法：简单移动平均法（Simple Moving Average）和加权移动平均法（Weighted Moving Average）。

移动平均的适用条件

　　移动平均（Moving Average）是一种简单平滑预测技术，通过在时间序列上逐项推移取一定项数的均值的方法来表现指标的长期变化和发展趋势。因为取的是一定项数的均值，所以使用移动平均的指标需要满足以下几个条件：

  • 指标没有明显的快速增长或下降的趋向
  • 指标不具备周期性波动的特征

　　移动平均的最重要目的是消除指标的随机波动，如果指标不满足以上的两个条件，可能移动均值的平滑能力无法对指标做出准确的预测，那么移动平均也就失去了它的效用。移动均值主要基于对历史数据的平滑来预测实际数据，所以一方面对于历史数据过度依赖，另一方面对于现实的变动不够敏感，尤其是在使用多期均值时，这也是移动均值的两个缺点。

简单移动平均法

　　简单移动平均（Simple moving average, SMA），将时间序列上前n个数值做简单的算术平均。假设用X1到Xn来表示指标在时间序列上前n期中每一期的实际值，那么第n+1期的预测值可以用以下公式来计算得到：

Xn+1 = ( X1 + X2 + …… + Xn ) / n

　　在Oracle数据库可以使用开窗函数直接计算得到简单移动平均值，比如要从每天的销售表（sales）计算近10天销售额（amount）的移动平均数与每天的销售额进行比较，可以用如下的PL/SQL实现：

SELECT date_id “日期”,SUM(amout) “每天销售额”,AVG(SUM(amount)) OVER(ORDER BY date_id ROWS BETWEEN 10 PROCEDING AND CURRENT ROW) “销售额移动均值” FROM sales GROUP BY date_id ORDER BY date_id;

　　Oracle内置了一堆的分析函数可以调用，直接用于各类的聚合和分析指标的计算，非常方便。

加权移动平均法

　　加权移动平均（Weighted moving average, WMA），在基于简单移动平均的基础上，对时间序列上前n期的每一期数值赋予相应的权重，即加权平均的结果。基本思想是：提升近期的数据、减弱远期数据对当前预测值的影响，使预测值更贴近最近的变化趋势。我们用Wn来表示每一期的权重，加权移动平均的计算公式如下：

Xn+1 = W1×X1 + W2×X2 + …… + Wn×Xn

　　这里需要满足W1+W2+……+Wn=1，对于各权重的确定，可以使用经验法根据需要进行赋权：如果希望预期值受前几期数据的影响逐步加深，则可以赋予递增的权重，如0.1,0.2,0.3……；如果希望加深最近期的几个数值的影响，以反映最近的变化，则可以适当加大近1-2期的权重，根据适应实际情况结合测试来完成赋权。我们来比较下简单移动平均（下图SMA线，取近5期均值）和加权移动平均（下图WMA线，取近5期加权均值，权重依次为0.1, 0.1, 0.2, 0.3, 0.3）：

SMA_WMA

　　可以看到无论是简单均值线还是加权均值线都要比实际值的波动小了很多，也就是平滑的效果，更多的是展现一个大体的趋势，而加权平均相较于简单平均的差异就在于加权平均更加注重近期的影响，所以这里的WMA绿线比SMA的红线更贴近前两期的数值趋势。

移动平均实例

　　还是结合实际的例子来做下说明。在电子商务数据分析里面，我们最关注的就是每天的销售额，我们用Excel里面的移动平均的趋势图可以反映出指标的变化趋势：

3per_Mov_Avg

——3周期移动平均（虚拟数据）

　　上面展现的是移动平均法的用途之一——分析趋势，其实我们也可以用移动平均来进行数据监控和预警。

　　用移动平均法可以计算得到一个本期的预测值，我们可以将这个预测值作为本期预期可以实现的量，并用这个预期量与实际量进行比较，要分析实际量与预期量之间的差距。还是基于销售额，不过销售额可能存在明显的递增或递减趋势，于是我们除以消费用户数，于是就得到了所谓的ARPU值（Average Revenue Per User），这个是电子商务乃至任何消费型网站的关键指标之一，还是使用简单移动平均来比较实际值和预期值的差异：

ARPU_SMA_diff

——ARPU监控表格效果（虚拟数据）

　　表格的数据展现已经可以一目了然的看到实际ARPU值与预期的差异、差异的大小等，下面再结合图表来看一下：

ARPU_SMA_diff_chart

——ARPU监控图表效果（虚拟数据）

　　两条比较的折线结合绿涨红跌的蜡烛图，能够对指标的变化情况了如指掌。结合上面的表和图的数据和效果，似乎对于数据的监控变得简单很多，即使是直接的观察也能快速地发现数据的异常，这些方法对于网站的一些关键指标，诸如转化率、人均消费、活跃度等指标的日常监控分析非常实用和有效。

　　如果你认为这些表和图对于指标监控还不够，那么就建一套自动的Alert系统吧，就像Google Analytics上面的Intelligence一样，如果指标的降幅或者涨幅超过正常范围（可以设定一个合理的阈值）就向你的邮箱发送报警邮件，这个对于敏感数据的监控异常有效。

　　我要介绍的就是这些了，切忌所有的方法和数据的处理都要根据实际的环境、具体的业务和运营状况来进行设定和分析，这里只是我的想法和对移动平均法的简单应用，在不同的环境下也许还可以扩展出许多不同的应用。你是不是也在用类似的方法？欢迎与我分享 :)

关键指标背后的秘密

18 条回复

secret-of-kpi　　前面的一篇文章介绍了可以用来评估KPI的数据上下文——质量控制图，通常我们会用KPI来衡量一些内容的质量、流量的质量，以及访问的质量等，我们经常根据KPI指标直接排序，并认为排在前几名的就是优质的内容，但其实这种方式并不是对所有的KPI都有效。举个最简单的例子：转化率Conversion Rate是很多网站的KPI指标，一般我们会让为Conversion Rate越高则渠道质量越好，或者内容质量越高，但有一种情况，如果网站内容普遍的转化率为10%，但有一个内容的访问次数一共2次，其中有一次实现了成功的转化，那该内容的转化率就是50%，是不是很“高”？是不是真的有这么高？

　　所以我们在分析关键指标的变化趋势，控制KPI的质量的时候，还需要注意一个问题，那就是如何运用KPI进行有效的评价。

　　其实Google Analytics已经给了我们答案，在前段时间推出了Weighted Sort（赋权排序）的功能，Avinash Kaushik先生在先前的博文——End of Dumb Tables in Web Analytics Tools! Hello: Weighted Sort对这个功能做过介绍，因为近段时间需要用到这个功能，但我的数据并不在GA上，所以我必须自己设计一套给关键指标赋权的体系，以发现到底这些KPI值可以达到多少预期，这里来分享下我的应用实例。

KPI期望值公式

　　还是以转化率Conversion Rate为例，电子商务中每个商品的转化率应该是：购买该商品成功的数量/该商品被浏览的次数，所以从统计学的角度来看，当商品的浏览次数（不妨叫做基数，数学上的集合元素个数或者统计学上的样本总数）这个基数越大时，转化率CR的置信度也就越高，同样是10%的转化率，浏览次数为1000的商品显然要比浏览次数只有100的商品在转化率这个数值上的可信度要高，统计学上称为“大数定理”。

　　根据上面的结论，我们需要根据每个商品转化率的真实值（Actual Value），权衡它的可信度，进而计算得到该商品转化率的期望值（Excepted Value），而这里的可信度就是真实值可以获得的权重，比如60%，那么还有个问题，既然是加权和，另外的40%的权重应该由什么来中和呢？参考GA中Weighted Sort的计算公式，用的是均值，也就是所有转化率的平均，非常不错的idea，于是我们可以得到以下公式了：

期望值（Excepted Value）=权重（Weight）×真实值（Actual Value）+（1-权重）×均值（Average Value）

　　我们看看哪些数据我们现在就可以拿到，权重显然还不行，真实值应该已经统计得到了，均值？既然有了所有的真实值，那么均值就是一个取平均的简单计算了。好的，那下面就说说我是如何来确定这个权重的。

权重的确定

　　先看看权重需要符合哪些原则，应该表现为怎样的一个特征。显然，权重的取值范围应该在[0,1]，也就是0到100%之间；另外，权重跟基数应该是正相关的，也就是基数越大，权重应该越大。如果你看过我之前的文章——数据的标准化，是不是已经想到了什么？是的，里面有几个公式可以直接用，简单地说，就是将基数进行归一化处理。

　　KPI的基数一般都是自然数，比如转化率的浏览次数、Bounce Rate的访问数，人均消费的用户数等，所以反正切函数atan不适用，min-max和log函数都适用，可以用散点图简单看一下分别用这两种方法归一化之后权重和基数的变化关系：

Min-max

min-max-plot

　　Min-max是直线的正相关，也就是权重和基数同比例地变化，变化速度一直。

Log函数

log-plot

　　Log函数是对数曲线的正相关，也就是权重的变化速度要比基数来得快。

　　根据这两个方法的特征，我选择了log函数作为权重的计算函数，因为它更符合基数和可信度之间的关系。

应用实例

　　既然KPI期望值的计算公式，及公式所有需要的数据都已经可以得到了，那么我们就来看看，KPI的基数是如何影响KPI的期望值的：

log-weight-fit

　　即基数越大，期望值越接近真实值，反之，则越接近平均值。算法和公式确定之后，我们就可以将其应用到实际的案例当中去了，这里以网站的转化率CR为例，看看这个KPI期望值的算法是不是有效的。

渠道 进入访问数 转化访问数 真实转化率 权重 期望转化率
渠道1 1534 118 7.69% 79.81% 7.51%
渠道2 9817 641 6.53% 100.00% 6.53%
渠道3 682 43 6.30% 70.99% 6.45%
渠道4 136 11 8.09% 53.45% 7.49%
渠道5 795 69 8.68% 72.65% 8.17%
总计 12964 882 6.80%    

　　表格中的例子是用转化率评价每个渠道流量的质量，比对加权前后的转化率情况，可以看到渠道4由于进入的访问数（基数）较小，所以预期的转化并没有真实值反映的那么好，甚至要差于渠道1；而渠道1因为基数较大，其真实转化率基本能够反映现实情况，渠道2因为基数最大，所以期望值就是实际值。

　　你也不妨试着用上述的方法转化下你的KPI，发掘一下KPI背后到底隐藏着哪些真相，也许你会发现转化后的结果更加可信，更加能让数据需求方所接受了，那么这个转变就成功了。不要忘了在评论中发表下尝试后的感想，分享下你的使用经历。