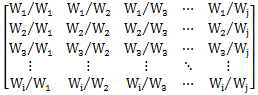分类目录归档：数据分析方法

数据分析方法介绍

参数估计与置信区间

　　我们总是希望能够从一些样本数据中去探究数据总体的表现特征，在网站数据分析中也是如此，我们试图从最近几天的数据表现来推测目前网站的整体形势是怎么样的，有没有变好或者变差的信号，但当前几天的数据无法完全代表总体，所以这里只能使用“估计”。同时，网站的数据始终存在波动，将最近时间段的数据作为抽样样本很可能数据正好处于较低或者较高水平，所以我们用样本得到的估计值不可能是无偏差的，我们同时需要去评估这个估计值可能的变化区间。

　　参数估计（Parameter Estimation）是指用样本的统计量去估计总体参数的方法，包括点估计和区间估计。

点估计

　　点估计（Point Estimation）是用抽样得到的样本统计指标作为总体某个未知参数特征值的估计，是一种统计推断方法。

　　一般对总体参数的估计会包括两类：一种是用样本均值去估计总体均值，对应到网站数据中的数值型指标，比如网站每天的UV，我们可以用近一周的日均UV去估计目前网站每天唯一访客数量的大体情况；另外一种是用样本概率去估计总体概率，对应到网站数据中的比率型指标，比如网站的目标转化率，我们可以用近3天的转化率去预估网站当天目标转化的水平；同时我们会计算样本的标准差来说明样本均值或者概率的波动幅度的大小，从而估计总体数据的波动情况。

　　点估计还包括了使用最小二乘法对线性回归做曲线参数的拟合，以及最大似然估计的方法计算样本集分布的概率密度函数的参数。

区间估计

　　区间估计（Interval Estimation）是依据抽取的样本，根据一定的正确度与精确度的要求，估算总体的未知参数可能的取值区间。区间估计一般是在一个既定的置信水平下计算得到总体均值或者总体概率的置信区间（Confidence Interval），一般会根据样本的个数和标准差估算得到总体的标准误差，根据点估计中用样本均值或样本概率估计总体均值或总体概率，进而得出一个取值的上下临界点。

　　我们可以将样本标准差记作S，如果我们抽样获取的有n个样本，那么总体的标准差σ就可以用样本标准差估算得到：

　　从这个公式中我们可以看到大数定理的作用，当样本个数n越大时，总体指标差σ越小，样本估计值越接近总体的真实值。Excel的图表里面也提供了添加“误差线”的功能：

　　有了总体的标准差σ，我们就可以使用区间估计的方法计算总体参数在一定置信水平下的置信区间，置信区间（Confidence Interval）给出了一个总体参数的真实值在一定的概率下会落在怎么样的取值区间，而总体参数落在这个区间的可信程度的这个概率就是置信水平（Confidence Level）。当抽取的样本数量足够大时（一般n>30），根据“中心极限定理”，我们可以认为样本均值近似地服从正态分布。

　　根据Z统计量的计算公式：

　　假如在1-α的置信水平下，则总体均值μ的置信区间为：

　　这里样本均值和标准差都可以根据抽样的结果计算得到，所以在既定置信水平的条件下，我们只要查Z值表（Z-Score）得到相应的Z值就可以计算得到总体均值的置信区间。对于置信水平或者叫置信度的选择，在统计学中一般认为95%的置信度的结果具有统计学意义，但其实在互联网领域数据的分析中不需要这么高的置信度，我们有时也会选择80%或者90%的置信度，相应的Z值见下表：

置信水平1-α	对应Z值Z_α/2
95%	1.96
90%	1.65
80%	1.28

　　对于总体概率的估计，在具备足够样本数量的条件下，我们用样本概率p预估总体概率，而总体概率的标准差则是sqrt(p(1-p)/n)，同样可以计算得到置信区间。

　　其实这篇文章的内容大部分都可以在统计学书籍或者网上Wiki里面找到，当然写到博客里面不是为了做科普，这里的每篇“数据分析方法”类目下的文章都是跟相应的网站数据分析的应用文章结合，这篇也不例外，如果你对相关内容感兴趣，请关注后续发布的文章，或者订阅我的博客吧。

多维交叉分析

4 条回复

　　我们在进行数据分析的时候，大部分时间都在使用趋势分析、比较分析、细分分析这三类方法，但其实还有一个方法我们也会经常使用——交叉分析，尤其是在排查数据异常的问题时，交叉分析就能展现其强大的威力。另外要跟大家说声抱歉的是博客的更新频率可能没有那么频繁了，但是尽量每个月至少能发布一篇，希望文章的质量有所保证，还是欢迎大家留言讨论，能够发起一些有趣的话题，一起拓展在网站数据分析方面的思路。

什么是交叉分析？

　　交叉分析是指对数据在不同维度进行交叉展现，进行多角度结合分析的方法，弥补了独立维度进行分析没法发现的一些问题。

　　交叉分析以多维模型和数据立方为基础，也可以认为是一种特殊的细分方式，但跟细分的概念有点差异，如果有兴趣可以先阅读下之前的文章——数据立方体与OLAP。细分的方法更多的是基于同一维度的纵深展开，也就是OLAP中的钻取（Drill-down），比如从月汇总的数据细分来看每天的数据，就是在时间维度上的细分，或者从省份的数据细分查看省份中各城市的数据，是基于地域维的下钻。交叉分析不再局限于一个维度，就像数据立方体与OLAP文章中的立方体，是基于不同维度的交叉，时间维、地域维和产品维交叉在一起分析每个小立方的数据表现，可以通过OLAP的切片（Slice）和切块（Dice）操作查看例如上海市在3月份的电子产品的销售情况，这会帮助我们发现很多在单个维度中无法发现的问题。所以，交叉分析是基于不同维度横向地组合交叉，而不是细分在同一维度的纵向展开。

交叉分析的展现形式

　　交叉分析涉及多维度的组合，虽然图表和表格都可以进行展现，但因为图表所能表达的数据有限，且比较不容易把多个维度的交叉关系展现出来，在交叉分析中不太常用，通常以表格为主。我们平常在看的表格通常被叫做二维表，一般第一列放置一个维度，如日期，表头罗列各类指标（其实所有指标也可以被认为是一种特殊的维度——指标维），这样行列的两个维就组成了最常见的二维表。二维表可以进行扩展，进而展现更加丰富的维度：

　　如上图就是典型的基于表格的多维度交叉分析的布局，在行列中分层次放置多个维度，如果我们只显示一个指标，那么这里的指标维就没有显示的必要了。其实Excel的数据透视表（Pivot Table）就是交叉分析的利器，我在数据的报表和报告这篇文章中提到过数据透视表，这里还是基于那篇文章截图的原始数据，如果我们将各维度按照上面的布局形式进行展现的话，会是怎么样的效果：

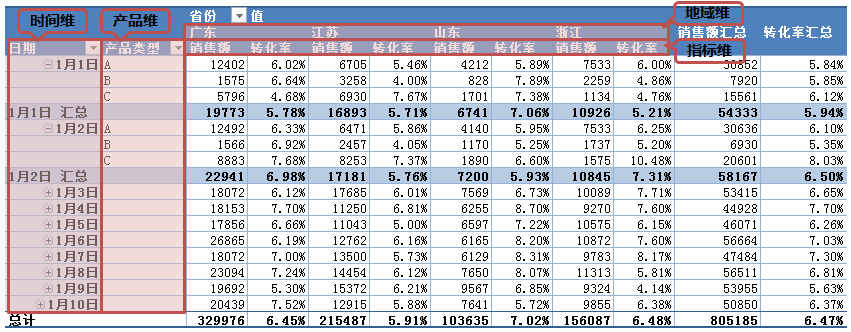
　　看起来还不错，显示的信息非常丰富，左边包含了以天为单位时间维和产品维，可以使用展开按钮进行汇总和展开，就像是细分的操作；上面的表头部分分两层罗列了地域维和指标维，Excel的透视表提供了丰富的设置，默认展现基于各个维度的汇总数据，让我们可以从“总-分”的角度观察数据，这对数据分析非常有用。假如我们使用上面的透视表进行交叉分析发现数据是否存在异常？

　　使用从总体到细节的分析方法，首先可以从查看每天销售额和转化率的汇总数据开始，折叠产品维之后观察最右侧的指标汇总列就可以看到每日汇总数据；如果某一天的销售额或转化率出现了大幅的下滑，我们就可以结合各种维度寻找问题的原因，就是基于各种维度的细节数据，展开产品维观察当天的哪类产品销售出现了问题，然后结合地域维的交叉数据，可以定位哪类商品在哪个省份的销售出现了问题，这样就有效地将问题定位到了细节的层面，能够更好地发现问题，进而解决问题。所以交叉分析其实正是体现了分析“分而析之”的本意。

　　上面的方法一般是比较常用的基于问题的分析方法，但我们很少可以一次就定位到问题，往往我们会根据推测多次查询数据库或查看Dashboard上的各类报表来定位问题。而结合透视表的交叉分析，我们使用一张报表就快速地定位了问题所在，从总体到细节，逻辑非常清晰，问题的定位也非常准确和到位，所以合理地利用交叉分析可以帮助我们更加高效地排查问题。

交叉分析的基础

　　这里不得不再说一下交叉分析基于的底层基础数据模型，因为如果没有设计好底层的数据模型，上层的交叉分析是很难实现的，或者多维的交叉受到限制而使分析存在局限性。

　　从技术层面来看，交叉分析基于多维模型，数据的维度越丰富，所能实现的交叉也越丰富和灵活，通过各种交叉分析能够更加有效地发现问题；但相应的，如果要尽可能地丰富各维度的交叉分析，对基层模型的要求也就越高。所以如何设计好数据的底层模型非常关键，还是引用数据立方体与OLAP文中的那个数据立方看个简单的例子：

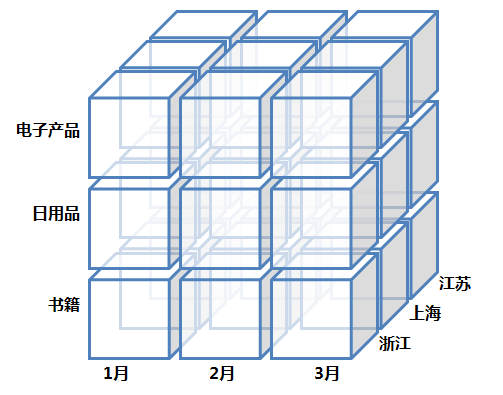
　　如果一张网站分析的报表只包含以月度为单位的日期维和相应的指标，那么数据的存储就是每个月一条记录，但显然这种高度聚合的数据不利于分析，我们需要构建如上图的数据立方体来获取更加细节的数据。用数据立方来拓展数据细节有两种方向，一类是纵深拓展，也就是基于一个维度的细分，比如将一个月细分到每一天，那么一条记录将会被拓展成30条；还有一种是横向的拓展，就是多个维度的交叉，就像上面立方中添加了产品维和地域维。这样存储的数据就从原本单一的时间维度扩展成了时间、产品和地域三个维度，也就是三维立方体所能展现的形式，当然维度可以继续扩展，四个五个直到N个，理论上都是可行的，这里只要以三个维度进行举例就可以。对于数据存储而言，横向的拓展与纵深拓展的影响是一样的，记录数都是以倍乘的方式增长，假设这里产品维是产品大类，有20个产品大类，再加上32个省份或直辖市，那么经过纵深和横向拓展之后，原先每月的1条记录就变成了：

1 × 30 × 20 × 32 = 19200

　　而我们在构建多维模型的时候很多维度中包含的数据量绝对不像上面例举的那么小，想象一下网站的商品或者页面的数量可能是成百上千甚至成千上万的，那么一旦以倍乘的形式扩展之后，数据量就会一下子剧增。虽然丰富的多维立方能够给分析带来便利，但也同时给数据的存储和查询带来的压力。

　　所以，更加丰富和灵活的分析需求的实现基于更加复杂的多维模型或者数据立方，同时会带来更大的系统开销。Google Analytics很好地权衡了灵活的数据分析与复杂数据模型之间的关系，这也是Google Analytics强大功能的基本保障，GA的高级细分（Advanced Segments）和自定义Dashboard是其他同类免费网站分析工具所无法比拟的，这也正是为什么我们将GA划分到网站数据分析工具，而其他的大部分只能算作网站数据统计工具的原因。而GA正是基于其构建的强大的底层数据模型和高效的数据计算和响应能力，使很多分析功能可以得到扩展，其中很多就涉及交叉分析，这里截图了其中的两个功能，Secondary Dimension和Pivot：

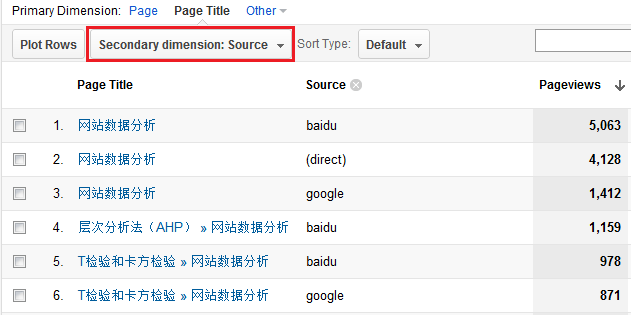
　　Google Analytics新版本增加了很多令人心动的功能，Secondary dimension的功能从老版本得到了延续，上图在Content模块的Page报表中选择了流量来源作为第二维度，这样我们就可以查看每个页面的流量是从何而来，每个流量来源在该页面的数据表现，同时可能还可以发现一些有趣的现象，比如某些页面的流量基本都是一个来源带来的，比如我的博客的某些文章基本都是通过搜索引擎进来的，而另外一些文章基本通过直接流量带来。

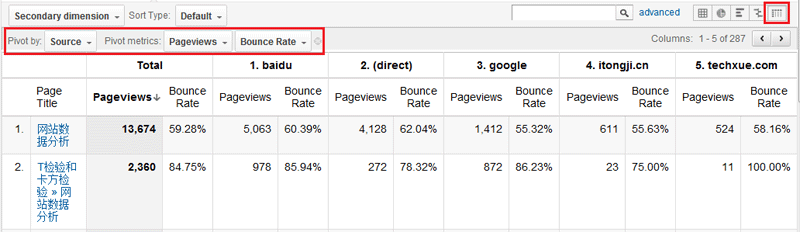
　　在GA的各类报表中可以在右上角选择展现的形式，最后的一种就是Pivot，Pivot的形式对表格的表头进行了扩展，可以分层次放置另外的维度，如上图还是使用了页面与流量来源的交叉，将Source维度放到了指标的上方。同时GA支持在两个维度的基础上最多选择两个度量Metric，我这里选择了Pageviews和Bounce Rate，来衡量每个页面中各类流量来源所带来的“量”和“质”，同样对于分析非常有价值。

　　多维的交叉分析我们在日常中潜移默化地经常会用到，交叉分析对于问题的排查和定位额外有效，所以我们需要想办法用更好的形式去展现数据，以便于更有利于进行交叉分析，其实这里介绍的透视表的方式是最常用的，也是比较好用的，但这类方式太少，不知道大家有没有其他更加有效的交叉分析展现方式。

T检验和卡方检验

32 条回复

　　好久没有更新博客了，今天更新一篇关于数据分析方法的文章，主要是基于统计学的假设检验的原理，无论是T检验还是卡方检验在现实的工作中都可以被用到，而且结合Excel非常容易上手，基于这类统计学上的显著性检验能够让数据更有说服力。还是保持一贯的原则，先上方法论再上应用实例，这篇文章主要介绍方法，之后会有另外一篇文章来专门介绍实际的应用案例。

关于假设检验

　　假设检验（Hypothesis Testing），或者叫做显著性检验（Significance Testing）是数理统计学中根据一定假设条件由样本推断总体的一种方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。既然以假设为前提，那么在进行检验前需要提出相应的假设：

　　H0：原假设或零假设（null hypothesis），即需要去验证的假设；一般首先认定原假设是正确的，然后根据显著性水平选择是接受还是拒绝原假设。

　　H1：备择假设（alternative hypothesis），一般是原假设的否命题；当原假设被拒绝时，默认接受备择假设。

　　如原假设是假设总体均值μ＝μ₀，则备择假设为总体均值μ≠μ₀，检验的过程就是计算相应的统计量和显著性概率，来验证原假设应该被接受还是拒绝。

T检验

　　T检验（T Test）是最常见的一种假设检验类型，主要验证总体均值间是否存在显著性差异。T检验属于参数假设检验，所以它适用的范围是数值型的数据，在网站分析中可以是访问数、独立访客数、停留时间等，电子商务的订单数、销售额等。T检验还需要符合一个条件——总体符合正态分布。

　　这里不介绍t统计量是怎么计算的，基于t统计量的显著性概率是怎么查询的，其实这些计算工具都可以帮我们完成，如果有兴趣可以查阅统计类书籍，里面都会有相应的介绍。这里介绍的是用Excel的数据分析工具来实现T检验：

　　Excel默认并没有加载“数据分析”工具，所以需要我们自己添加加载项，通过文件—选项—加载项—勾选“分析工具库”来完成添加，之后就可以在“数据”标签的最右方找到数据分析这个按钮了，然后就可以开始做T检验了，这里以最常见的配对样本t检验为例，比较某个电子商务网站在改版前后订单数是否产生了显著性差异，以天为单位，抽样改版前后各10天的数据进行比较：

	改版前订单数	改版后订单数
1	1032	1187
2	1178	1245
3	1098	1379
4	1045	1094
5	976	1173
6	1101	1364
7	1276	1119
8	1215	1268
9	987	1303
10	1065	1274

　　首先建立假设：

H0：μ₁＝μ₂，改版前后每天订单数均值相等；
H1：μ₁≠μ₂，改版前后每天订单数均值不相等。

　　将数据输入Excel，使用Excel的数据分析工具，选择“t检验：平均值的成对二样本分析”，输出检验结果：

　　看到右侧显示的结果是不是有点晕了，看上去有点专业，其实也并不难，只要关注一个数值的大小——单尾的P值，这里是0.00565，如果需要验证在95%的置信水平下的显著性，那么0.00565显然小于0.05(1-95%)，拒绝零假设，认为改版前后的订单数存在显著性差异。简单说下为什么选择单尾显著性概率P，而不是双尾，对于大部分网站分析的应用环境，我们一般需要验证改动前后数值是否存在明显提升或下降，所以一般而言只会存在一类可能——或者提升或者下降，所以只要检验单侧的概率即可，就像上面例子中改版后的订单数均值1240.6大于改版前的1097.3，我们需要验证的就是这种“大于”是否是显著的，也就是做的是左侧单边检验，这种情况下只要关注单尾的显著性概率P即可。

卡方检验

　　卡方检验（chi-square test），也就是χ²检验，用来验证两个总体间某个比率之间是否存在显著性差异。卡方检验属于非参数假设检验，适用于布尔型或二项分布数据，基于两个概率间的比较，早期用于生产企业的产品合格率等，在网站分析中可以用于转化率、Bounce Rate等所有比率度量的比较分析，其实在之前的文章——Abandonment Rate的影响因素进行过相关的应用。这里同样不去介绍χ²是如何计算得到的，以及基于χ²统计量的显著性概率的查询等，这里直接以转化率为例来比较网站改版前后转化率是否发生了显著性差异，抽样改版前后各3天的网站分析数据——总访问数和转化的访问数，用“转化访问数/总访问数”计算得到转化率：

	改版前	改版后
总访问数	30567	33651
转化访问数	2976	3698
转化率	9.74%	10.99%

　　首先建立假设：

H0：r₁＝r₂，改版前后转化率相等；
H1：r₁≠r₂，改版前后转化率不相等。

　　其实这是一个最简单的四格卡方检验的例子，也无需使用SPSS（当然你足够熟悉SPSS也可以使用类似的统计分析工具），为了简化中间的计算步骤，我这里用Excel直接制作了一个简单的卡方检验的模板，只要在相应的单元格输入统计数据就能自动显示检验的结果：

点击下载：卡方检验示例

　　Excel中浅蓝色的单元格都支持输入，包括原用方案和测试方案的总访问数和转化访问数，另外置信度95%也是支持修改了，如果你需要99%的置信水平，只要修改这个单元格即可。

　　怎么看检验结果？其实非常简单，只要看那个红色的“存在”单元格的显示结果即可，上面的案例中两者的转化率“存在”显著性差异，如果不存在，则该单元格相应的就会显示“不存在”，有了这个模板对于A/B Testing等类似的数据比较也显得非常简单容易，或者说其实这个Excel模板就是为了A/B Testing而量身定制的。

　　好了，就到这里吧，其实这篇文章并不是想从专业的统计学的角度来介绍T检验和卡方检验，只是想让大家了解这两个方法的原理和适用条件，能够用最简单的方式去使用诸如此类的方法让数据更具说服力，请继续关注之后奉上的应用实例。

质量控制图

13 条回复

　　其实之前的一篇文章——网站数据分析的基本流程介绍过质量管理（Quality Management, QM）相关的内容，只是介绍的是概念和流程这类比较定性的东西，这篇文章也是跟质量管理相关的内容，但介绍的主要是定量分析相关的工具——质量控制图。

质量控制图的概念与用处

　　如果要系统地介绍，可能要从质量管理(Quality Management,QM)开始，从传统的质量管理七工具，到全面质量管理阶段的6σ管理，这里不去展开，只介绍质量控制图。

　　质量控制图，简称控制图（Control Chart），是质量管理七工具之一，由美国的贝尔电话实验所的休哈特(W.A.Shewhart)博士在1924年首先提出，因此也称为“休哈特控制图”。最初的应用当然是在生产领域，使用抽样的方式检验产品的质量是否处于控制状态。一般而言，指标的波动受随机因素和系统因素的影响，如果指标只受到随机因素的影响，那么在正常情况下指标的变化状态是稳定的、可控的，但如果发生某种系统性的变化就会使指标超出原先可控的波动范围，处于失控状态，所以控制图就是帮助我们及时发现这种失控状态，从而进行及时的调整。

　　质量控制图通过统计上均值μ和标准差σ的状况来衡量指标是否在稳定状态，同时选择3σ来确定一个正常波动的上下限范围（根据正态分布的结论，指标的特征值落在μ±3σ之间的概率是99.73%），使用均值μ作为控制图的中心线（Center Line, CL），用μ+3σ作为控制上限（Upper Control Limit, UCL），用μ-3σ作为控制下限（Lower Control Limit, LCL），如图。

　　根据衡量的指标数值类型的差异，质量控制图主要分为两类：计数型控制图和计量型控制图，下面分别介绍其中的一种：

质量控制图具体用法

　　因为生产制造业和互联网行业存在着较大差异，所以这里只介绍适合用于网站分析的2个控制图。其中计数型控制图中主要介绍P控制图，主要用于定类型变量，即符合二项分布检验“是否”的变量，如用户是否完成交易、用户是否为新用户……这类指标一般会以比率的形式出现，如转化率、新用户比例等，而P控制图正是衡量这些比率是否出现异常（在生产行业通常用于不合格率等）；另外的计量型控制图主要用于一些关键的数值度量，如每个订单的消费额、每个用户的下载次数等，这类指标在网站分析中通常计算全部数据的均值来观察波动情况，其实计量型控制图最常用的是均值-极差（X-R）和均值-标准差（X-S）控制图，但两者都是通过取样的方式实现的，并且每次取样的样本数最好能保持相等，所以这类抽样统计不太适合于上述网站分析中的指标，这里介绍个相对能够普遍适用并且计算也没有那么复杂的图——单值-移动极差（X-MR）控制图。下面一个个来，先是P控制图：

P控制图

　　根据中心极限定理规律，当二项分布的样本容量足够大时，分布趋向正态N(ρ, ρ(1-ρ)/n)（这里用ρ先暂代下p均值，上横线很难打出来，具体见下面图中公式），所以总体均值μ就是ρ，方差σ²就是ρ(1-ρ)/n，进而就可以计算得到中心线CL、控制上限UCL、控制下限LCL：

p-chart-expression

–p_k：每组样本的比例值，n_k：每组样本容量

　　我在这里使用了UCL_k和LCL_k，也就是每组样本都有各自的控制上限和控制下面，当然我们也可以跟CL一样使用统一的UCL和LCL，这时n不再使用每组的样本容量，而是使用每组样本容量取均值的结果，只是简单的变换，公式就不贴出来了。

X-MR控制图

　　第二类计量型控制图中的单值-移动极差（X-MR）控制图，需要先计算指标的移动极差：MR=|X_i-X_i-1|，即每个数值减去前一个相邻的数据的绝对值，进而计算指标均值和移动极差均值，通过公式转换算出均值X控制图和移动极差MR控制图的CL、UCL、LCL：

x-MR-Chart-expression

–x_i、MR_i：每个个体的数值和计算得到的极差，k：样本个体数，d₂、D₃、D₄：极差到标准差的转化系数，相当于n=2的极差转化系数，所以在这里可以看作是固定值。

　　通过套用上面的公式，可以计算得到相应的CL、UCL、LCL，结合每个特征值就可以画出控制图。因为这篇文章主要基于方法，同时也主要是为下一篇文章作为技术铺垫，所以不具体举例了，具体实例见之后的——网站KPI的质量控制，这里先附上一张维基百科上的质量控制图：

质量控制图的控制规则

　　既然质量控制图是为了帮助我们及时发现指标的不正常状态，那么当我们看到上面的图以后，需要观察和分析是不是存在异常的点或异常的变化趋势，如何定义这些异常，需要有一套控制规则：即样本点出界或者样本点排列异常：

点超出或落在ULC或LCL的界限；（异常）
近期的3个点中的2个点都高于+2σ或都低于-2σ，近期5个点中的4个点都高于+σ或都低于-σ；（有出现异常的趋势）
连续的8个点高于中心线或低于中心线；（有偏向性）
连续的6个点呈上升或者下降趋势；（有明显的偏向趋势）
连续的14个点在中心线上下呈交替状态。（周期性，不稳定）

　　查资料时发现不同的地方对控制规则有不同的定义，我这里参照的是SPSS里面的规则，具体应该可以根据实际的应用环境进行调整。

　　看到这里，你是不是会发现质量控制图其实很有用，结合图比对这些规则后能够很快地发现指标的异常和可能产生的异常，一目了然。具体应用会在近几天内一并奉上，请继续关注。

层次分析法（AHP）

42 条回复

　　层次分析法（Analytic Hierarchy Process）简称AHP，是美国运筹学家T. L. Saaty教授于70年代初期提出的， AHP是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法。它的特点是把复杂问题中的各种因素通过划分为相互联系的有序层次，使之条理化，根据对一定客观现实的主观判断结构(主要是两两比较)把专家意见和分析者的客观判断结果直接而有效地结合起来，将每个层次元素两两比较的重要性进行定量描述。而后，利用数学方法计算反映每一层次元素的相对重要性次序的权值，通过所有层次之间的总排序计算所有元素的相对权重并进行排序。

层次分析法的适用范围

　　层次分析法适用于多目标决策，用于存在多个影响指标的情况下，评价各方案的优劣程度。当一个决策受到多个要素的影响，且各要素间存在层次关系，或者有明显的类别划分，同时各指标对最终评价的影响程度无法直接通过足够的数据进行量化计算的时候，就可以选择使用层次分析法。

AHP的模型结构

　　首先，可以根据实际问题构建层次模型，这里以网站质量的衡量为例来简单说明下，我们可以认为网站质量主要由网站内容的质量及网站交互的友好度决定，而内容的质量又受到内容的完整性、准确性和及时性的影响；交互的友好度由交互流程的友好度及网站的整体信息架构的优良程度来决定，所以可以构建如下图的模型：

　　为了计算各要素对上一层指标的影响权重（如内容的准确性对内容质量的影响程度有多高，需要计算出该权重，而完整性、准确性和及时性3个指标对内容质量的影响权重的和为1，其它各指标也同样满足该原则），需要构建对比矩阵，即从模型的第二层开始运用9标度对从属于上一层中每个要素的同层各要素间进行两两比较，如模型中的要素i相对于要素j对上层要素的重要程度，1表示i与j同等重要，3表示i比j略重要，5表示i比j重要，7表示i比j重要很多，9表示i比j极其重要，可以用W_i/W_j表示该重要程度，两两比较后可以得到以下矩阵：

　　因为上面的矩阵是通过两两比较的结果列出来的，所有对于整个矩阵而言不一定是完全一致的，所以首先需要验证该对比矩阵的一致性。可以通过计算矩阵的最大特征值的方法来衡量矩阵的一致性，相关的指标有一致性指标CI，随机一致性指标RI，一致性比率CR=CI/RI（具体的计算方法不详细介绍了，可以参考相关资料）。一般当CR<0.1时，我们认为该对比矩阵的一致性是可以被接受的。

　　如果矩阵的一致性满足要求，则可以根据矩阵的最大特征值进一步计算得到对应的特征向量，并通过对特征向量进行标准化（使特征向量中各分量的和为1）将其转化为权向量，也就是我们要求的结果，权向量中的各分量反映了各要素对其相应的上层要素的影响权重。如：

　　网站质量=内容质量*0.6+交互友好*0.4

　　内容质量=完整性*0.3+准确性*0.4+及时性*0.3

　　交互友好=交互流程*0.7+信息架构*0.3

　　在计算得到各要素相对于上层要素的权重之后，我们就可以通过加权平均的方法将最底层指标的测量结果汇总到目标指标的最总分值，用于评价各决策方案的优劣性，并选择最优方案。如：

　　网站质量=（完整性*0.3+准确性*0.4+及时性*0.3）*0.6+（交互流程*0.7+信息架构*0.3）*0.4

层次分析法的应用前提

　　在应用层次分析法时，必须满足以下几个前提：

各层的要素必须是已知的，并且条理结构清晰，能够按层次区分排列；
同一层中的各要素的关系是平等的，而各要素间相互独立，不存在显著的相关性；
最底层的指标可以被量化，并能够通过一定的方法测量；
需要明确各层次间要素的影响关系。

数据的标准化

53 条回复

　　数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

　　其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上，常见的数据归一化的方法有：

min-max标准化(Min-max normalization)

　　也叫离差标准化，是对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下：

　　其中max为样本数据的最大值，min为样本数据的最小值。这种方法有一个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。

log函数转换

　　通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

　　看了下网上很多介绍都是x^*=log₁₀(x)，其实是有问题的，这个结果并非一定落到[0,1]区间上，应该还要除以log₁₀(max)，max为样本数据最大值，并且所有的数据都要大于等于1。

atan函数转换

　　用反正切函数也可以实现数据的归一化：

　　使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上。

　　而并非所有数据标准化的结果都映射到[0,1]区间上，其中最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法：

z-score 标准化(zero-mean normalization)

　　也叫标准差标准化，经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：

　　其中μ为所有样本数据的均值，σ为所有样本数据的标准差。